Assalammu‘alaikum wr. wb.
Hello gaes! Apakah kalian juga termasuk Phobia Matematika? Kali ini jangan takut untuk berhitung. Sekarang di Kelas 12 ini saya akan menjelaskan tentang Dimensi Tiga (Bangun Ruang) dan Statistika untuk Pelajaran Matematika Wajib.
DIMENSI TIGA (KEDUDUKAN DAN TITIK PADA BANGUN RUANG)
1. Kedudukan Titik, Garis, dan Bidang dalam Dimensi Tiga
Dimensi tiga terbentuk dari 3 Elemen yaitu Titik, Garis, dan Bidang. Titik adalah Lukisan tanda Noktah yang dibubuhi nama menggunakan Huruf Kapital. Suatu Titik tidak memiliki besaran dan tidak berdimensi. Garis adalah Himpunan Titik-titik yang hanya memiliki ukuran panjang dan berdimensi Satu. Sedangkan bidang adalah Himpunan Titik-titik yang memiliki Ukuran panjang dan luas, sehingga dikatakan berdimensi dua. Bidang adalah Luasan (Bidang Datar), dan hanya dapat dibentuk dari :
- Tiga Titik berbeda
- Satu Titik dan Satu Garis
- Dua Garis yang Berpotongan atau Sejajar.
Contoh Titik, Garis, dan Bidang digambarkan di bawah ini :
Suatu Titik, Garis, ataupun Bidang memiliki suatu posisi atau kedudukannya satu sama lain. Kedudukan ini mempunyai syarat-syarat khusus yaitu sebagai berikut :
1.) Kedudukan Titik terhadap Garis
a. Titik terletak pada Garis
Titik berada pada Garis karena Garis itu melalui Titik. Contohnya titik A, P, dan titik B pada gambar 2.
b. Titik berada di luar Garis
Titik berada di luar Garis karena Garis itu tidak melalui Titik. Contohnya titik Q.

2.) Kedudukan Titik terhadap Bidang
Titik berada pada bidang terjadi karena :
- Bidang melalui titik.
- Titik berada pada garis yang terletak pada bidang itu.
Contohnya titik P
3.) Titik berada di luar Bidang
Titik berada di luar bidang terjadi karena :
- Bidang tidak melalui titik
- Titik tidak berada pada garis yang berada pada bidang itu.
Contohnya titik Q

4.) Kedudukan Garis terhadap Bidang adalah sebagai berikut :
- Garis berada terletak pada bidang contohnya garis AB,AC, dll (gambar 4). Garis berada pada bidang karena ada dua titik yang dilalui garis pada bidang itu.
- Garis memotong atau menembus bidang yaitu contohnya garis PQ. Garis menembus / memotong bidang karena ada satu titik yang dilalui garis pada bidang itu (Titik Tembus).
- Garis sejajar dengan bidang contohnya garis RS. Garis sejajar dengan bidang karena garis itu sejajar dengan salah satu garis pada bidang itu atau tidak memiliki satupun titik persekutuan.

5.) Kedudukan Bidang terhadap Bidang lain
a. Dua Bidang yang saling Sejajar.
Dua bidang sejajar apabila tidak ada satupun garis berpotongan bidang dari kedua bidang.

b. Dua Bidang saling Berpotongan
Dua bidang berpotongan apabila terdapat Garis Perpotongan Bidang, yaitu garis persekutuan yang merupakan bagian dari kedua bidang.

c. Dua Bidang saling Terimpit
Dua Bidang saling Terimpit (α, β). Apabila setiap titik yang terletak pada bidang α juga terletak pada bidang β atau setiap titik yang terletak pada bidang β juga terletak pada bidang α.

Kedudukan Titik, Garis dan Bidang memiliki suatu Aksioma. Aksioma adalah sebuah pernyataan dimana pernyataan yang kita terima sebagai suatu kebenaran dan bersifat umum. Tanpa perlu adanya pembuktian dari kita sendiri. Aksioma terhadap kedudukan Garis, dan bidang adalah sebagai berikut :
- Apabila dua buah bidang berpotongan tegak lurus, maka seluruh garis dari bidang 1 terhadap Bidang 2 juga Tegak Lurus.
- Hasil Perpotongan dua bidang adalah garis, sedangkan hasil Perpotongan tiga bidang dapat berupa Garis atau Titik.
2. Proyeksi Titik dan Garis Pada Bidang
Proyeksi adalah Proses Penjatuhan (Pemindahan) titik dan garis pada suatu bidang. Proyeksi dapat disebut juga dengan pencerminan. Proyeksi dilakukan dengan cara menjatuhkan titik atau titik tersebut pada Garis tegak lurus terhadap Bidang, dan biasanya dilambangkan dengan Tanda Aksen (‘). Berikut di bawah ini adalah bentuk-bentuk proyeksi titik atau garis ke suatu bidang.



3. Jarak dari Titik ke Titik, Titik ke Garis, dan Titik ke Bidang
Jarak adalah Panjang Ruas Garis penghubung kedua bangun itu yang terpendek dan bernilai Positif.
a. Jarak antara Titik dan Titik
Jarak antara titik A dan titik B adalah panjang Ruas Garis AB.

b. Jarak antara titik dan garis
Jarak antara titik A dan garis g (titik A terletak di luar garis g) adalah panjang ruas garis AA’, dengan titik A’ merupakan proyeksi titik A pada garis g. Dengan perkataan lain jarak antara titik A dan garis g ditentukan dengan cara menarik garis dari titik A tegak lurus garis g sehingga memotong garis g dititik A’, maka garis AA’ adalah jarak antara titik A dan garis g. (Lihat Gambar 11 (a)).
Jika garis g terletak pada suatu bidang dan titik A berada di luar bidang tersebut, maka untuk menentukan jarak antara titik A dan garis g ditempuh dengan membuat garis AB yang tegak lurus bidang, kemudian tariklah garis BC yang tegak lurus garis g, sehingga diperoleh panjang ruas garis AC yang merupakan jarak antara titik A dan garis g. (Lihat Gambar 11 (b)).

c. Jarak antara titik dan bidang
Jarak antara titik A dan bidang α adalah panjang ruas garis AA’. Dengan titik A’ merupakan proyeksi titik A pada bidang α.
Karena AA’ ⊥ a dan AA’ b, maka hasilnya adalah AA’ bidang α.

4. Jarak Dua Garis Sejajar, Jarak Garis dan Bidang Yang Sejajar, Jarak Dua Bidang Sejajar
a. Jarak Dua Garis Sejajar
Jarak antara garis g dan h yang sejajar adalah garis AB, dengan titik A adalah sebarang titik pada garis g dan titik B merupakan proyeksi titik A pada garis h.

b. Jarak antara garis dan bidang yang sejajar
Jarak antara garis g dan bidang α = panjang ruas garis AB (AB tegak lurus bidang α dan garis g).

c. Jarak dua bidang yang saling sejajar
Bidang α sejajar dengan bidang β maka jarak kedua bidang = panjang ruas garis AB (AB tegak lurus dengan kedua bidang).

5. Sudut Antara Garis dan Bidang
Sudut adalah kemiringan yang dihasilkan antara garis dengan garis atau garis dengan bidang. Sudut pada dimensi tiga biasa disimbolkan dengan α, β, atau θ. Jika garis b tidak tegak lurus pada bidang α maka sudut antara garis b dan bidang α adalah sudut lancip yang dibentuk oleh garis g dan proyeksi garis g pada bidang α.
- Jika garis B tegak lurus pada bidang α maka sudut antara garis b dan bidang α adalah 900
- Jika garis B terletak pada bidang α atau sejajar dengan bidang α maka sudut antara garis B dan bidang α adalah 00

6. Sudut Antara Garis dan Bidang
Sudut antara dua bidang (yang berpotongan) adalah sudut yang terbentuk oleh dua garis pada masing-masing bidang tadi di mana setiap garis itu tegak lurus pada garis potong kedua bidang tersebut di satu titik.
Garis (α, β) = perpotongan bidang α dan β.
AB dan BC tegak lurus (α, β)

Untuk lebih lanjut tentang Rumus-rumus Bangun RUang, silahkan bacalah di bagian selanjutnya.
DIMENSI TIGA (BANGUN RUANG)
Sumber Materi : Studiobelajar.com, Brainly
A. Ciri-ciri Bangun Ruang
1. Kubus
Kubus merupakan Bangun Ruang yang dibatasi oleh 6 Bujur sangkar yang saling Kongruen. Keenam bujur sangkar disebut sisi kubus dan garis yang menjadi perpotongan dua sisi kubus disebut rusuk kubus. Kubus memiliki 12 Rusuk yang sama panjang.

- Volume kubus :
- Luas permukaan :
Ciri-ciri Kubus :
- Memiliki 6 buah bidang yang berbentuk persegi yang kongruen yang terdiri dari sisi alas, sisi atas dan 4 sisi selimut
- Memiliki 12 rusuk yang sama panjang
- Memiliki 8 buah titik sudut
- Memiliki 12 diagonal bidang
- Memiliki 4 diagonal ruang
- Memiliki 6 bidang diagonal
2. Balok
Balok memiliki 6 Sisi dimana masing-masing sisi yang berhadapan saling kongruen. Balok memiliki 12 Rusuk dengan 3 kelompok panjang yang berbeda yaitu p, l, dan t seperti dibawah:

- Volume :
- Luas permukaan :
Ciri-ciri Balok :
- Memiliki 6 buah bidang yang berbentuk persegi atau persegi panjang yang terdiri dari 3 pasang sisi yang sejajar, saling berhadapan dan kongruen
- Memiliki 12 rusuk yang terdiri dari 4 rusuk panjang, 4 rusuk lebar dan 4 rusuk tinggi
- Memiliki 8 buah titik sudut
- Memiliki 12 diagonal bidang
- Memiliki 4 diagonal ruang
- Memiliki 6 bidang diagonal
3. Prisma
Prisma adalah bangun ruang yang memiliki 2 bidang yang sejajar dan kongruen yang disebut penampang. Bidang yang menghubungkan kedua penampang disebut selimut prisma.

- Volume :
- Luas permukaan :
Ciri-ciri Prisma segi n beraturan :
- Memiliki (n + 2) buah bidang yang terdiri dari n buah bidang selimut yang berbentuk persegi panjang, 2 bidang yang sejajar dan kongruen yang berbentuk segi n sebagai bidang alas dan bidang atas
- Memiliki 2n buah titik sudut
- Memiliki 3n buah rusuk yang terdiri dari rusuk alas, rusuk atas dan tinggi prisma
- Memiliki n(n – 1) buah diagonal sisi
- Memiliki n(n – 3) diagonal ruang
- Memiliki ½ n(n – 1) bidang diagonal jika n genap dan ½ n(n – 3) bidang diagonal jika n ganjil
4. Limas
Limas merupakan bangun ruang yang terdiri dari satu bidang alas dan selimut bangun yang berbentuk bidang-bidang segitiga. Satu titik dari masing-masing segitiga saling bertemu di sebuah titik disebut titik puncak limas.

- Volume :
- Luas permukaan :
Ciri-ciri Limas segi n beraturan :
Memiliki (n + 1) buah sisi/bidang yaitu n buah sisi tegak yang berbentuk segitiga dan sebuah sisi alas yang berbentuk segi n beraturan
Memiliki (n + 1) buah titik sudut yaitu n titik sudut alas dan 1 titik puncak
Memiliki 2n buah rusuk yaitu n buah rusuk alas dan n buah rusuk tegak limas
Tidak semua limas memiliki diagonal bidang, diagonal ruang dan bidang diagonal
5. Silinder / Tabung
Silinder merupakan bangun ruang yang memiliki 2 Bidang penampang berbentuk lingkaran yang sejajar dan kongruen. Bidang selimut silinder merupakan bidang persegi panjang yang dilengkungkan secara mulus mengikuti keliling bidang lingkarannya.

- Volume :
- Luas permukaan :
Ciri-ciri Tabung :
- Memiliki sisi alas dan sisi atas yang berbentuk lingkaran yang kongruen, saling berhadapan dan sejajar
- Memiliki sisi selimut yang berbentuk persegi panjang
- Memiliki 2 buah rusuk lengkung
- Tidak memiliki titik sudut
6. Kerucut
Kerucut merupakan bidang ruang yang terdiri dari satu bidang alas lingkaran dan sebuah titik puncak dengan selimut bidang berbentuk juring lingkaran dan busurnya dilengkungkan semulus keliling lingkarannya.

- Volume :
- Luas permukaan :
- Luas permukaan :
Ciri-ciri Kerucut :
- Memiliki 2 sisi yaitu sisi alas yang berbentuk lingkaran dan sisi selimut yang berbentuk juring lingkaran
- Memiliki sebuah rusuk lengkung
- Memiliki sebuah titik sudut sebagai titik puncak
7. Bola (Sphere)
Bola merupakan bangun ruang yang tidak mempunyai bidang alas dan titik pojok. Bola merupakan himpunan titik dalam dimensi tiga yang memiliki jarak sama terhadap satu titik tertentu yang disebut pusat bola. Jarak pusat bola ke titik-titik permukaan lingkaran disebut jari-jari bola.

- Volume :
- Luas permukaan :
Ciri-ciri Bola :
- Memiliki sebuah sisi lengkung sebagai sisi selimut
- Tidak mempunyai rusuk
- Tidak mempunyai titik sudut
B. Contoh Soal Jarak Titik Bangun Ruang
Konsep dalam menghitung jarak titik ke titik pada dimensi tiga mungkin sudah kita pahami. Untuk memperdalam pemahaman mengenai bagaimana cara menghitung jarak dari titik ke titik pada Dimensi Tiga, ayo kita coba kerjakan contoh soal di bawah.
1.) Suatu Ruangan berbentuk Kubus ABCD.EFGH dengan Panjang Rusuk 20 m. Tentukan jarak dari titik A ke C dan jarak dari titik A ke G. Langkah pertama adalah menggambar kubus ABCD.EFGH untuk memudahkan mengerjakan soal.
Sekarang mari kita amati titik A dan C. Jarak titik A ke titik C adalah panjang ruas AC, yang mana merupakan diagonal bidang atau diagonal sisi pada kubus tersebut. Perhatikan gambar di bawah untuk mengilustrasikan panjang ruas AC.
Maka, panjang diagonal bidang atau jarak antara titik A ke titik C adalah 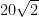 m. Sekarang mari kita ilustrasikan titik A dan G. Jarak antara titik A dengan G merupakan panjang diagonal ruang kubus.
m. Sekarang mari kita ilustrasikan titik A dan G. Jarak antara titik A dengan G merupakan panjang diagonal ruang kubus.
Jika kita perhatikan, diagonal ruang tersebut membentuk segitiga ACG, dimana AC merupakan diagonal bidang yang telah kita cari sebelumnya, dan CG merupakan rusuk dari kubus itu sendiri. Perhatikan gambar di bawah untuk mengilustrasikan panjang ruas AG.
2.) Simak ilustrasi di bawah ini. Jarak titik A dengan bidang p, dimana titik A berada di luar bidang p, adalah panjang garis AA'. Titik A' diperoleh dari proyeksi titik A pada bidang p, yang mana titik A harus tegak lurus dengan bidang p.
Mari simak studi kasus pada bangun ruang kubus di bawah agar kita dapat menerapkan konsep menentukan titik dengan bidang pada dimensi tiga.
Misalkan diketahui kubus ABCD.EFGH seperti gambar di atas, dengan panjang rusuknya adalah 6 cm. Titik A, titik D, titik G, dan titik F dihubungkan sehingga membentuk bidang ADGF. Coba tentukanlah jarak antara titik B ke bidang ADGF. Dikutip dari Mathematical Dictionary (1857), langkahnya adalah dengan menentukan panjang ruas garis yang tegak lurus bidang ADGF dan melalui titik B. Mari perhatikan ilustrasi proyeksi titik B ke bidang ADGF.
Pada gambar, panjang ruas BT adalah tegak lurus bidang ADGF. Maka jarak titik B ke bidang ADGF adalah ruas garis BT. Panjang ruas BT jika diamati, memiliki bentuk segitiga ATB, dimana siku-siku di titik T.
Panjang AT adalah panjang setengah dari diagonal bidang ABFE, yaitu 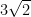 . Sehingga selanjutnya kita dapat menentukan panjang ruas BT dengan menggunakan Teorema Phytagoras :
. Sehingga selanjutnya kita dapat menentukan panjang ruas BT dengan menggunakan Teorema Phytagoras :
STATISTIKA PART 1
Sumner Materi : Quipper.com (Blog), Yuvalianda.com, Ruangguru.com (Blog), Studiobelajar.com, dan Dosenpendidikan.co.id
Pengolahan Informasi Statistik mempunyai sejarah jauh ke belakang sejak awal peradaban manusia. Pada awal Zaman Masehi, bangsa-bangsa mengumpulkan Data Statistik untuk mendapatkan informasi deskriptif mengenai banyak hal, misalnya Pajak, Perang, Hasil Pertanian, dan bahkan Pertandingan Atletik.
Pada masa kini dengan berkembangnya teori peluang kita dapat menggunakan berbagai metode statistik yang memungkinkan kita meneropong jauh di luar data yang kita kumpulkan dan masuk kedalam wilayah pengambilan keputusan melalui Generalisasi dan Peramalan.
Dalam kehidupan sehari-hari, terdapat banyak data yang dapat menginformasikan sesuatu. Data-data tersebut hanya akan berakhir sebagai data saja, apabila tidak diolah terlebih dahulu. Ilmu Statistika berperan mengumpulkan, mengolah hingga mengambil kesimpulan dari suatu data.
Ada 2 (Dua) Bagian dari Statistika yang akan mengolah data tersebut, yaitu Statistika deskriptif dan Statistika Inferensia. Kedua bagian tersebut memiliki peranan masing-masing dalam hal pengumpulan data hingga pengambilan kesimpulannya. Statistika deskriptif yang bertugas mengolah dan menyajikan data, sedangkan Statistika Inferensia lebih terfokus pada proses Uji Analisis hingga pengambilan keputusan.
Dalam hal ini, akan dipelajari mengenai Statistika deskriptif yang berbicara tentang Metode-metode Pengumpulan, Pengolahan, dan Penyajian Data sehingga dapat memberikan gambaran informasi yang jelas dan menarik. Kemampuan mengolah dan menyajikan data sangat dibutuhkan sebagai langkah awal dalam mempelajari Ilmu Statistika, karena dari penyajian data tersebutlah akan didapatkan informasi yang lebih jelas sehingga dapat dilakukan penganalisisan lebih lanjut.
A. Pengertian Statistika
Statistika adalah Ilmu yang mempelajari semua hal tentang Data, mulai Pengumpulan, Penyajian, Analisis, sampai terbentuk suatu Kesimpulan. Statistika merupakan ilmu yang harus dikuasai "Because everything need Statistics".
Contohnya, menghitung Rata-rata Nilai Ujian, menentukan banyaknya Siswa yang suka membolos, menghitung tingkat kepatuhan Siswa pada Peraturan Sekolah, menghitung Tingkat Penularan COVID-19 (Ataupun Data Statistik Pasien COVID-19) di suatu Lokasi, menentukan Laju Inflasi, dan masih banyak lainnya. Saat belajar Statistika, Anda akan mengenal istilah Populasi dan Sampel. Apa itu?
1. Populasi
Populasi adalah Objek yang dijadikan Penelitian. Misalnya, jika kamu akan melakukan Penelitian tentang pengaruh Hormon Steroid pada pertumbuhan Ayam Pedaging (Broiler), maka populasi yang dipilih adalah Ayam Pedaging yang dibudidayakan oleh Peternak.
2. Sampel
Sampel adalah bagian dari Populasi yang bisa dijadikan sebagai Sumber Informasi. Misalnya, dari banyaknya Ayam Pedaging yang dimiliki oleh Peternak, Anda cukup mengambil beberapa saja untuk kamu amati selama Proses Penelitian. Artinya, kamu tidak perlu menjadikan semua Ayam sebagai Bahan Penelitian.
B. Kategorisasi Ilmu Statistika
Terdapat 2 Kategori besar dalam Ilmu Statistika. Apa sajakah itu?
1. Statistika Deskriptif
2. Statistika Inferensial
Statistika Inferensial adalah metode untuk menyatakan keterkaitan antara kesimpulan dan populasi yang diteliti berdasarkan Informasi dari Sampel. Contoh Statistika Inferensial bisa Anda lihat pada saat Quick Count / Real Count Pemilu Pilpres, Pilgub atau Pilkada.
[Untuk membacanya lebih lanjut, silahkan lihat di sini.]
C. Perhitungan Statistika Dasar (Mean, Modus, dan Median)
Ukuran Gejala Pusat Data belum dikelompokkan dimaksudkan sebagai besaran atau ukuran untuk mendapatkan gambaran yang lebih jelas berdasarkan letak data dari sekumpulan data yang di punyai. Untuk lebih mengetahui dan mengerti tentang materi ini, silahkan tonton Video di YouTube di bawah ini :
Adapun yang termasuk pada ukuran Gejala Letak antara lain adalah :
1.) Mean (Rataan Hitung)
Mean adalah nilai rata-rata dari beberapa buah data. Nilai mean dapat ditentukan dengan membagi jumlah data dengan banyaknya data.
Mean (Rata-rata) merupakan suatu ukuran pemusatan data. Mean suatu data juga merupakan statistik karena mampu menggambarkan bahwa data tersebut berada pada kisaran mean data tersebut. Mean tidak dapat digunakan sebagai ukuran pemusatan untuk jenis data nominal dan ordinal.
a. Rataan Data Tunggal
b. Rataan Data Kelompok [Sumber : Rumusstatistik.com]
Median adalah nilai data tengah (dengan pengertian, bahwa dari sekelompok data dibagi menjadi dua bagian yang sama dan pembagi nya disebut sebagai median). Adapun untuk menentukan nilai median dapat dilakukan dengan cara untuk data yang belum di kelompokkan.
Langkah pertama yang harus dilakukan adalah melakukan penyusunan data berdasarkan urutan data dimulai dari data terkecil sampai data terbesar, lalu tentukan median nya sesuai dengan jumlah data nya (ganjil atau ganjil). Untuk sekumpulan data yang berjumlah ganjil maka nilai median nya adalah merupakan data yang paling tengah dan untuk sekumpulan data yang berjumlah genap, maka median nya adalah jumlah dua data tengah di bagi 2 (Dua).
*) Median untuk Jumlah Data (n) Ganjil
Keterangan :
Me = Median
n = jumlah data
x = nilai data
b. Median Data Kelompok [Sumber : Rumusstatistik.com]
Modus digunakan untuk gejala gejala yang sering terjadi, diberikan dengan simbol Mo. Modus dalam data kuantitatif ditentukan dengan melihat Frekunsi tertinggi. Untuk Modus Data Tunggal, tinggal lihat saja yang paling sering muncul. Dan untuk yang Modus Data Berkelompok ada Rumus-rumusnya, yaitu :
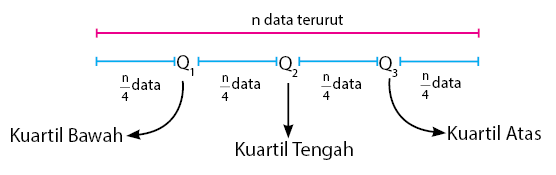
Nilai Kuartil merupakan nilai dari sekumpulan data yang di bagi menjadi 4 (Empat) bagian yang sama dan membagi data tersebut dinamakan Kuartil. Menentukan nilai-nilai kuartil tersebut di bagi menjadi dua kategori yaitu nilai nilai kuartil untuk data yang belum di kelompokan ke dalam daftar distribusi frekuensi dan nilai-nilai kuartil yang sudah di kelompokan ke dalam daftar distribusi frekuensi.
Berdasarkan gambar diatas, bawah dapat kita ketahui letak – letak kuartilnya, yaitu pada Kuartil Bawah (Q1), Kuartil Tengah (Q2) dan Kuartil Atas (Q3).
Untuk lebih memahami dari Materi ini, tontonlah Video di YouTube di bawah ini :
a. Kuartil Data Tunggal
Dalam mencari nilai kuartil untuk Data Tunggal, Rumus dibedakan menjadi 2 Kasus, yaitu untuk Jumah Data Ganjil dan Jumlah Data Genap.
Sedangkan cara untuk mencari n Genap, yaitu :
Langkah – langkah mencari tiga nilai kuartil data tunggal untuk jumlah data genap ialah sebagai berikut :
b. Kuartil Data Kelompok
Tb adalah Tepi bawah kuartil ke-i
F adalah Jumlah frekuensi sebelum frekuensi kuartil ke-i
f adalah Frekuensi kuartil ke-i. i = 1, 2, 3
n adalah Jumlah seluruh frekuensi
C adalah Panjang interval kelas
c. Simpang Kuartil
Yang dimaksud dengan Simpangan Kuartil adalah jangkauan dari ketiga kuartil itu sendiri. Kamu bisa menghitung Simpangan Kuartil dengan Rumus berikut :

a. Desil Data Tunggal
Keterangan :
adalah desilk e-i
adalah banyaknya data
b. Desil Data Kelompok
Keterangan :
adalah desil ke-i
adalah tepi bawah kelas kuartil
adalah panjang kelas
adalah banyak data
adalah frekuensi kumulatif sebelum kelas kuartil
adalah frekuensi kelas kuartil
a. Persentil Data Tunggal
Keterangan :
adalah pesentil ke-i
adalah banyaknya data
b. Persentil Data Kelompok
Keterangan :
adalah persentil ke-i
adalah tepi bawah kelas persentil
adalah panjang kelas
adalah banyak data
adalah frekuensi kumulatif sebelum kelas persentil
adalah frekuensi kelas persentilE. Simpang Rata-rata dan Simpang Baku
Untuk lebih memahami dari Materi ini, tontonlah Video di YouTube di bawah ini :
Simpangan Rata-rata (Deviation Mean) adalah Rata-rata jarak antara nilai-nilai data menuju rata-ratanya. Simpangan Rata-rata termasuk ke dalam ukuran penyebaran data seperti halnya varian dan standar deviasi. Kegunaannya adalah untuk mengetahui seberapa jauh nilai data menyimpang dari rata-ratanya.
a. Simpang Rataan Tunggal
Simpangan rata-rata didefinisikan oleh :dimana adalah nanyaknya data, tanda menyatakan nilai mutlak (misal ), adalah nilai data ke- dan adalah rata-rata. Rata-rata diperoleh dari
b. Simpang Rataan Berelompok
Rumus simpangan rata-rata untuk data berkelompok adalah sebagai berikut.
dimana adalah simpangan rata-rata, adalah banyaknya kelas interval, adalah frekuensi kelas interval ke-, adalah nilai titik tengah kelas interval ke- adalah Rata-rata Data berkelompok yang dirumuskan olehdan tanda | ... | adalah tanda absolut yang menandakan bahwa semua nilai diubah menjadi nilai positif, jika nanti di dalamnya diperoleh nilai negatif, maka nilai tersebut harus dipositifkan.
Simpangan Baku atau juga yang sering kita kenal dengan nama Deviasi Standar (Standard Deviation) adalah ukuran persebaran data. Simpangan ini bisa diartikan jarak rata-rata penyimpangan antara nilai hasil pengukuran dengan nilai rata-rata .
a. Simpang Baku Tunggal
Simpangan baku atau standar deviasi (S) adalah rata-rata jarak penyimpangan titik-titik data diukur dari nilai rata-rata data tersebut. Simpangan baku dapat ditentukan dengan Rumus :

b. Simpang Baku Kelompok
Sedangkan untuk data berkelompok, Simpangan baku atau standar deviasi dapat ditentukan dengan Rumus :
Ragam atau varian  menyatakan rata-rata kaudrat jarak suatu data terhadap rataannya.
menyatakan rata-rata kaudrat jarak suatu data terhadap rataannya.
a. Variasi Tunggal
Rumus untuk mendapatkan Ragam atau Varian / Variasi Tunggal adalah :
b. Variasi Tunggal
Atau
Dengan :
 = banyak kelas
= banyak kelas
 = titik tengah kelas ke-i
= titik tengah kelas ke-i
 = nilai rata-rata
= nilai rata-rata
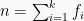
Rumus diatas dapat diubah dengan menggunakan simpangan rataan menjadi :
STATISTIKA PART 2
Sumner Materi : Tambahpinter.com
A. Penyajian Data
1. Distribusi Frekuensi
Untuk menyajikan data menjadi Tabel Distribusi Frekuensi, ada beberapa hal yang harus di tentukan :
a.) Menentukan Jangkauan (J)
Keterangan :
Xmax
= Data Terbesar
Xmin = Data Terkecil
Xmin = Data Terkecil
b.) Menentukan Banyak Kelas (K)
c.) Menentukan Panjang Kelas (C)
d.) Menentukan Batas kelas
Tepi bawah (Tb) = Batas bawah – 0,5
Tepi atas (Ta) = Batas atas + 0,5
Setelah mengelompokkan Data ke dalam bentuk Tabel Distribusi Frekuensi, kamu dapat menyajikan data kelompok tersebut ke bentuk diagram. Penyajian data dengan bentuk diagram atau grafik ini, dapat memudahkan pembaca dalam membaca data-data dan dapat memudahkan dalam menganalisa data yang disajikan.
Terdapat 3 macam Grafik untuk mempresentasikan Data Kelompok dan beserta contohnya :
1. Histogram
Pada poligon frekuensi, angka yang digunakan bukan Batas Bawah atau Batas Atas, tetapi Titik Tengah. Cara mencari Titik Tengah adalah dengan menjumlah tepi bawah dan tepi atas kemudian dibagi 2. Secara matematis dapat dituliskan sebagai berikut :
3. Ogive
Nilai ujian akhir mata pelajaran Matematika siswa kelas XII SMAN 1 dapat dilihat di bawah ini.
Pembahasan :
Langkah Pertama :

a. Distribusi Frekuensi
Dan jika mau melihat Rumus Statistika dalam Bahasa lainnya untuk Postingan di Instagram, silahkan lihat di sini :
Statistics (Math W) (Instagram Post) (Indonesian, English, Nederlands, and Germany)
Sumber : Canva [Statistics (Math W) (Instagram Post) (Indonesian, English, Nederlands, and Germany)]
Demikianlah semoga membantu khususnya untuk menyelesaikan soal Mata Pelajaran Matematika Wajib Kelas 12.
Mohon maaf apabila ada sedikit Kesalahan, baik itu Salah Kata, ataupun Salah menulis Rumus.Terima Kasih 😀👍 :)
Wassalammu‘alaikum wr. wb.


















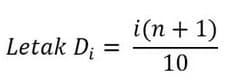
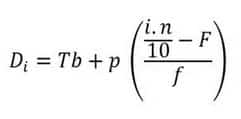
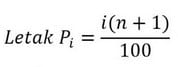
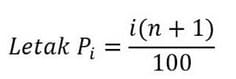











Post a Comment