Assalamu‘alaikum Wr. Wb.
Halo gais! Tentunya kita semua bertemu dengan Logika baik itu di dalam kehidupan sehari-hari maupun di dalam Pemrograman khususnya bagi Programmer dan Anak IT. Kali ini saya akan memberikan Materi Logika dan Aljabar Boolean untuk Mata Kuliah (Matkul) Matematika Diskrit (Matdis).
LOGIKA MATEMATIKA
Sumber Materi : Passinggrade.co.id, Belajarstatistics.com, Studiobelajar.com, Rumuspintar.com, Mathcyber1997.com, Uniksharianja.com, dan Gambarsoalterbaru.blogspot.com
Logika matematika adalah cabang ilmu yang digunakan untuk membuktikan suatu kebenaran. Materi ini bertujuan untuk menarik kesimpulan yang tidak hanya didasarkan pada logika alamiah, tapi juga Logika Ilmiah. Hukum-hukum Logika membantu kita membedakan antara argumen yang valid dan tidak valid. Logika juga digunakan untuk membuktikan teori-teori di dalam Matematika.
Logika Matematika sangat dekat kaitannya dengan pernyataan dan penarikan kesimpulan. Itulah sebabnya saat belajar materi ini kalian harus tahu apa yang disebut proposisi. Proposisi adalah suatu pernyataan yang mempunyai dua kemungkinan nilai kebenaran, yaitu benar atau salah tetapi tidak mungkin keduanya (lebih dari satu).
Dalam logika matematika, kita belajar untuk menentukan nilai dari suatu pernyataan, baik bernilai benar atau salah. Pernyataan sendiri terbagi menjadi 2 jenis, yaitu :
1. Pernyataan Tertutup (Kalimat Tertutup)
Pernyataan tertutup atau kalimat tertutup adalah suatu pernyataan yang sudah memiliki nilai benar atau salah.
Contoh :
“5 adalah bilangan genap”, kalimat tersebut bernilai salah karena yang benar adalah “5 adalah bilangan ganjil”.
2. Pernyataan Terbuka (Kalimat Terbuka)
Pernyataan terbuka atau kalimat terbuka adalah suatu pernyataan yang belum dapat ditentukan nilai kebenarannya karena adanya suatu perubah atau variabel.
Contoh Logika Matematika :
Saat 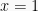 , maka
, maka  bernilai salah
bernilai salah
Saat 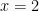 , maka
, maka 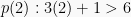 bernilai benar
bernilai benar
A. Ingkaran atau Negasi dari suatu Pernyataan
Ingkaran atau negasi adalah kebalikan nilai dari suatu pernyataan, dimana ketika suatu pernyataan bernilai benar, maka negasinya bernilai salah dan saat suatu pernyataan bernilai salah, negasinya bernilai benar. Ingkaran atau negasi dari pernyataan p dilambangkan dengan 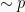 .
.
B. Pernyataan Kuantor
Pernyataan kuantor adalah bentuk logika matematika berupa pernyataan yang memiliki kuantitas. Dalam pernyataan kuantor, pada umumnya terdapat kata semua, seluruh, setiap, beberapa, ada, dan sebagian.
Kata-kata yang senilai dengan seluruh, semua, setiap termasuk dalam kuantor universal dan kata-kata yang senilai dengan sebagian, beberapa, ada termasuk dalam kuantor eksistensial. Kuantor universal dan kuantor eksistensial saling beringkaran.
p : Semua orang adalah sarjana (Kuantor universal)
~p : Sebagian orang adalah tidak sarjana
C. Pernyataan Majemuk, Bentuk Ekuivalen dan Ingkaran-nya
Dalam logika matematika, beberapa pernyataan dapat dibentuk menjadi satu pernyataan dengan menggunakan kata penghubung logika seperti dan, atau, maka dan jika dan hanya jika. Pernyataan gabungan tersebut disebut dengan pernyataan majemuk.
Dalam Logika Matematika, kata hubung tersebut masing-masing memiliki lambang dan istilah sendiri.
1. Tabel Kebenaran Konjungsi
Inilah contoh dari Tabel Kebenaran Konjungsi :
Dari tabel diatas dapat disimpulkan bahwa sifat dari konjungsi adalah bernilai benar jika kedua pernyataan penyusun dari pernyataan majemuk keduanya bernilai benar.
Dari tabel diatas dapat disimpulkan bahwa sifat dari disjungsi adalah bernilai salah jika kedua pernyataan penyusun dari pernyataan majemuk keduanya bernilai salah.
b. Tabel Kebenaran Implikasi
Pada sifat implikasi ini, p ⇒ q, p disebut sebagai hipotesis dan q sebagai konklusi. Pada implikasi ini akan bernilai salah ketika konklusi salah dan hipotesis benar.
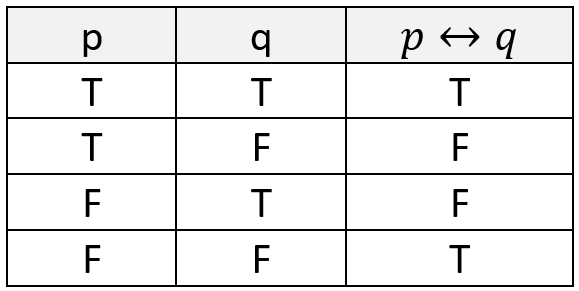
c. Tabel Kebenaran Biimplikasi
Pada Sifat Biimplikasi, pernyataan majemuk akan bernilai benar jika kedua pernyataan penyusunnya bernilai sama, keduanya benar atau keduanya salah.
2. Tautologi dan Kontradiksi
Tautologi adalah pernyataan majemuk yang selalu benar untuk semua kemungkinan yang ada dan kontradiksi adalah kebalikannya, yaitu pernyataan majemuk yang bernilai salah untuk semua kemungkinan yang ada.
3. Bentuk Ekuivalen Pernyataan Majemuk
Pernyataan majemuk yang memiliki nilai sama untuk semau kemungkinannya dikatakan ekuivalen. Notasi ekuivalen dalam logika matematika adalah “≡“.
Bentuk-bentuk pernyataan yang saling Ekuivalen adalah :
4. Ingkaran Pernyataan Majemuk
- Ingkaran Konjungsi :
- Ingkaran Disjungsi :
- Ingkaran Implikasi :
- Ingkaran Biimplikasi :
D. Konvers, Invers dan Kontraposisi
Konvers, Invers dan Kontraposisi adalah bentuk lain dari implikasi, dimana :
- Konvers dari
adalah
.
- Invers dari
adalah
.
- Kontraposisi dari
adalah
.
Dan inilah Tabel Kebenaran Biimlikasi (Konvers, Invers dan Kontraposisi) :
Contoh :
Tentukan Konvers, Invers, dan Kontraposisi dari "Jika terpapar COVID-19, maka lakukan Isolasi Mandiri."!
p : Terpapar COVID-19
q : Isolasi Mandiri
Implikasi :
p→q : Jika terpapar COVID-19, maka lakukan Isolasi Mandiri.
Konvers :
q→p : Jika melakukan Isolasi Mandiri, maka terpapar COVID-19.
Invers :
~p→~q : Jika tidak melakukan Isolasi Mandiri, maka tidak terpapar COVID-19.
Kontraposisi :
~q→~p : Jika tidak Isolasi Mandiri, maka tidak terpapar COVID-19.
E. Hukum Aljabar Proposisi
Hukum hukum aljabar proposisi aturan penggantian setiap proposisi yang saling ekivalen dapat dipertukarkan atau diganti antara satu dengan yang lainnya.
F. Penarikan Kesimpulan (Logika Matematika)
Penarikan kesimpulan adalah konklusi dari beberapa pernyataan majemuk (premis) yang saling terkait. Dalam penarikan kesimpulan terdiri dari beberapa cara, yaitu :
G. Tabel Kebenaran Logika
Berikut, inilah beberapa Contoh dari Tabel Kebenaran Logika.
p ∨ q
p ∧ q
~p
(p ∨ q) ∨ ~q
p ∨ ~(p ∧ q)
(p ∧ q) ∧ ~(p ∨ q)
(~p ∧ ~q) ∨ (p ∨ ~q)
(p ∧ q) ∧ ~(p ∨ q)
p → q
H. Contoh Soal Logika
Berikut ini merupakan Soal dan Pembahasan mengenai Logika Matematika.
1. Urutan nilai kebenaran dari ~p ∧ q adalah ....
A. BSSS D. SSSB
B. SBSS E. SSSS
C. SSBS
Jawaban dan Pembahasan :
Buatlah tabel kebenaran. Kolom pertama untuk p, kolom kedua untuk q, kolom ketiga untuk ~p, dan kolom terakhir untuk ~p ∧ q Pernyataan konjungsi akan bernilai BENAR ketika dan keduanya bernilai BENAR.
Dari kolom terakhir, kita peroleh bahwa urutan nilai kebenaran dari ~p ∧ q adalah SSBS (dibaca dari atas ke bawah).
(Jawaban C)
2. Urutan nilai kebenaran dari p ↔ (q ∨ ~p) adalah ....
A. BSSS D. BBBS
B. BSBB E. SSSB
C. SSBB
Jawaban dan Pembahasan :
Buatlah tabel kebenaran. Kolom pertama untuk p, kolom kedua untuk q, kolom ketiga untuk ~p, kolom keempat untuk q ∨ ~p, dan kolom terakhir untuk p ↔ (q ∨ ~p) Pernyataan Biimplikasi akan bernilai BENAR ketika dan keduanya memiliki nilai kebenaran yang sama.
Dari kolom terakhir, kita peroleh bahwa urutan nilai kebenaran dari p ↔ (q ∨ ~p) adalah BSSS (dibaca dari atas ke bawah).
(Jawaban A)
3. Jika p bernilai benar dan q bernilai salah, maka pernyataan majemuk di bawah ini yang tidak bernilai benar adalah ....
A. p ∨ q
B. p ∧ ~q
C. ~p → q
D. ~p ∧ q
E. ~(p → q)
Jawaban dan Pembahasan :
Diketahui p benar (B) dan q salah (S).
Cek semua opsi yang ada.
(Jawaban D)
4. Manakah dari pernyataan majemuk berikut yang bernilai salah?
A. 33
= 27 atau 32 = 8
B. 11 adalah bilangan prima atau 1P adalah bilangan kelipatan 5.
C. Sudut lancip kurang dari 90° atau 53 = 25.
D. Denpasar ada di Bali atau Surabaya merupakan ibu kota Jawa Tengah.
E. Tahun Kabisat ada 365 Hari atau Satu Tahun terdiri dari 52 Minggu.
Jawaban dan Pembahasan :
Semua pernyataan majemuk di atas dihubungkan oleh disjungsi dan akan bernilai benar ketika “cukup” salah satu pernyataan tunggal bernilai benar.
Opsi A :
p : 33 = 27 (B)
q : 32 = 8 (S)
Opsi B :
p : 11 adalah Bilangan Prima (B)
q : 10 adalah Bilangan Kelipatan 5 (B)
Opsi C :
p : Sudut lancip kurang dari 90° (B)
q : 53 = 25 (S)
Opsi D :
p : Denpasar ada di Bali (B)
q : Surabaya merupakan ibu kota Jawa Tengah (S)
Opsi E :
p : Tahun Kabisat ada 365 Hari (S)
q : Satu Tahun terdiri dari 52 Minggu (S)
Karena kedua pernyataan tunggal bernilai salah, maka pernyataan majemuk tersebut bernilai salah.
(Jawaban E)
5. Pernyataan yang senilai dengan “Jika UMR naik, maka semua harga sembako naik” adalah ....
A. Jika UMR tidak naik, maka semua harga sembako tidak naik
B. Jika UMR tidak naik, maka ada harga sembako yang tidak naik
C. Jika ada harga sembako yang tidak naik, maka UMR tidak naik
D. Jika semua harga sembako tidak naik, maka UMR tidak naik
E. Jika ada harga sembako yang naik, maka UMR tidak naik
Jawaban dan Pembahasan :
Pernyataan yang senilai (ekuivalen) dengan bentuk implikasi adalah kontraposisinya, yaitu
p→q ≡ ~q→~p
Perhatikan bahwa :
p : UMR naik
q : Semua harga sembako naik
~p : UMR tidak naik
~q : Ada harga sembako yang tidak naik
Dengan demikian, pernyataan yang senilai adalah “Jika ada harga sembako yang tidak naik, maka UMR tidak naik.”
(Jawaban C)
[Untuk melihat Soal lainnya, silakan lihat di sini (Mathcyber1997.com).]
ALJABAR BOOLEAN
Sumber Materi : Byjus.com, Webstudi.site, Allaboutcomputers123go.wordpress.com, Teknikelektronika.com, Sulistiawan03.blogspot.com, dan Matkul.xyz
Aljabar Boolean hanya mengenal dua keadaan, yaitu keadaan “True”/benar dan keadaan “False”/Salah. Dalam Aljabar Boolean keadaan ini ditunjukan dengan elemen dalam himpunan bilangan biner, yaitu 1 dan 0 (B = {1,0}), dan elemen tersebut dinyatakan dalam variabel peubah yang ditulis/dipilih dari huruf alfabet. Aljabar Boolean juga memiliki operasi logika yang berfungsi memberi batasan dari suatu keadaan sehingga suatu keadaan tidak dapat berada dalam dua ketentuan sekaligus. Operasi logika yang dimaksud adalah operasi dasar AND, OR, dan NOT. Kaidah operasi logika di perlihatkan dalam sebuah tabel kebenaran. Tabel kebenaran merupakan daftar semua kombinasi Bilangan Biner (1 & 0).
A. Hukum Aljabar Boolean
Dibawah inilah Hukum Aljabar Boolean.
B. Fungsi Aljabar Boolean
Berdasarkan penjelasan sebelumnya, maka gerbang dasar AND, OR, NOT 2 input akan menghasilkan 16 Fungsi yang ditunjukkan pada tabel dibawah.
Dalam menyelesaikan permasalahan yang berkaitan dengan Aljabar Boolean dua dan tiga variabel maka digunakan sifat identitas, disamping itu prinsip dualitas juga digunakan pada sifat-sifat identitas.
C. Operasi Aljabar Boolean Dua Variabel dan Tiga Variabel
Dalam menyelesaikan permasalahan yang berkaitan dengan aljabar Boolean dua dan tiga variabel maka digunakan sifat identitas, disamping itu prinsip dualitas juga digunakan pada sifat-sifat identitas.
Jika A, B, dan C adalah Variabel Boolean maka maka berlaku hukum/sifat berikut.
1. Hukum Komutatif
Hukum Komutatif menjelaskan bahwa penukaran atau perubahan urutan variabel input atau sinyal masukan sama sekali tidak mempengaruhi Variabel Output suatu Rangkaian Logika.
2. Hukum Asosiatif
Hukum Asosiatif menjelaskan bahwa perubahan urutan penyelesaian operasi pada variabel tidak akan mempengaruhi Variabel Output suatu Rangkaian Logika.
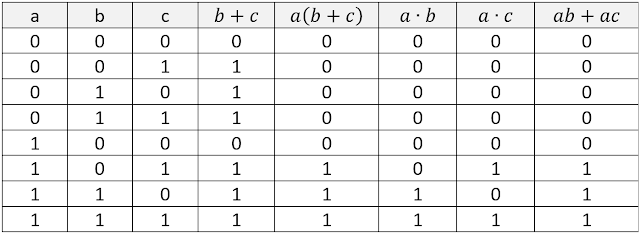
3. Hukum Distributif
Hukum Distributif menyatakan bahwa variabel input pada operasi aljabar Boolean dapat disebarkan tempatnya tanpa mengubah Variabel hasil dari Output suatu Rangkaian Logika.
4. Hukum Absorbsi, Kombinasi, dan Konsensus
Atau lebih lengkapnya, bisa lihat Infografik di bawah ini :
D. Teorema Aljabar Boolean
Dua Teorema penting yang sangat banyak digunakan dalam aljabar Boolean adalah hukum Pertama Demoorgan dan hukum kedua De Morgan. Kedua teorema ini digunakan untuk mengubah ekspresi boolean. Teorema ini pada dasarnya membantu untuk mengurangi ekspresi boolean yang diberikan dalam bentuk yang disederhanakan. Kedua hukum Demoorgan ini digunakan untuk mengubah ekspresi dari satu bentuk ke bentuk lain. Sekarang, mari kita bahas kedua Teorema ini secara rinci.
1. Hukum Pertama De Morgan
Hukum I De Morgan menyatakan bahwa (A∙B)’ = A’+B’. Hukum pertama menyatakan bahwa komplemen produk variabel sama dengan jumlah komplemen individu variabelnya. Tabel kebenaran yang menunjukkan pembuktian hukum pertama Demogan diberikan sebagai berikut :
Dua kolom terakhir menunjukkan bahwa (A∙B)’ = A’+B’. Oleh karena itu, Hukum Pertama De Morgan terbukti.
2. Hukum Kedua De Morgan
Hukum Kedua De Morgan menyatakan bahwa (A+B)’ = A’∙B'. Hukum Kedua menyatakan bahwa komplemen dari jumlah variabel sama dengan produk dari komplemen individu mereka dari suatu variabel. Tabel kebenaran berikut menunjukkan bukti untuk hukum kedua De Morgan.
Dua kolom terakhir menunjukkan bahwa (A+B)’ = A’∙B'. Oleh karena itu, Hukum Kedua De Morgan terbukti. Teorema lain dalam Aljabar Boolean adalah Teorema Komplementer, Teorema Dualitas, Teorema Transposisi, Teorema Redundansi dan sebagainya. Semua Teorema ini digunakan untuk menyederhanakan Ekspresi Boolean yang diberikan. Ekspresi Boolean yang dikurangi harus setara dengan Ekspresi Boolean yang diberikan.
E. Bentuk Kanonik pada Aljabar Boolean
Sumber : Sulistiawan03.blogspot.com dan Matkul.xyz
Definisi Aljabar Boolean adalah struktur aljabar yang "mencakup intisari" operasi logika AND, OR dan NOR dan juga teori himpunan untuk operasi Union (Gabungan), Interseksi (Irisan) dan Komplemen. Boolean adalah suatu tipe data yang hanya mempunyai dua nilai, yaitu True atau False (Benar atau Salah). Simbol yang digunakan pada Aljabar Boolean itu sendiri adalah (∙) untuk AND, (+) untuk OR dan (⨁) untuk NOR. Berikut, inilah Hukum-hukum Aljabar Boolean :
Untuk dapat memperoleh ekspresi Boolean yang harus diperhatikan hanyalah “output = 1”. Suku-suku bentuk SOP disebut minterm. sedangkan Untuk mendapatkan mendapatkan bentuk POS (maxterm) diperhatikan hanyalah “keluaran bernilai 0”.
1. Tabel Boolean Bentuk Baku dan Ikonik
Tabel kebenaran adalah tabel yang memuat semua kemungkinan atau kombinasi masukan serta keluaran dari kombinasi tersebut. pada umumnya tabel kebenaran yang memiliki nilai “n” masukan mempunyai 2n.
Membuat ekspresi Boolean dalam bentuk SOP dan POS dari Tabel Kebenaran berikut ini :
Penyelesaian :
a.) Dalam bentuk SOP, maka yang dilihat adalah Y = 1
b.) Dalam bentuk POS, maka yang dilihat adalah Y = 0

2. Bentuk Kanonik
Ada 2 macam Bentuk Kanonik, yaitu :
- Penjumlahan dari Hasil Kali (Sum-of-Product atau SOP)
- Perkalian dari Hasil Penjumlahan (Product-of-Sum atau POS)
Bentuk Kanonik merupakan Fungsi Boolean yang diekspresikan dalam bentuk SOP (Sum of Product) atau POS (Product of Sum) dengan minterm/maxterm. Kanonik memiliki literal yang lengkap. Sedangkan bentuk baku merupakan Fungsi Boolean yang diekspresikan dalam bentuk SOP atau POS dengan minterm atau maxterm mempunyai literal yang tidak lengkap. Untuk dalam memahami secara lengkap SOP (Sum of Product) diistilahkan dengan jumlah dari hasil perkalian. POS (Product of Sum) diistilahkan dengan perkalian dari hasil penjumlahan.
f(x, y, z) = x’y’z + xy’z’ + xyz → SOP
[Setiap suku (term) disebut minterm]
g(x, y, z) = (x + y + z)(x + y’ + z)(x + y’ + z’)
(x’ + y + z’)(x’ + y’ + z) → POS
[Setiap suku (term) disebut maxterm]
Setiap Miniterm/Maxterm mengandung Literal lengkap
Beberapa Bentuk Kanonik fungsi Boolean 3 masukan Variabel :
F. Tabel Aljabar Boolean
Berikut, inilah beberapa Contoh dari Tabel Kebenaran Aljabar Boolean.
x'
x'y+xy'+y'
xy'+z
Sebenarnya dulu, untuk Materi Logika sudah dipelajari di Matematika SMA. Karena Kurikulum baru, di SMA tidak lagi mempelajari tentang Logika Matematika. Akan tetapi, di dalam Tes masuk PTN seperti UTBK/SBMPTN juga ada sedikit Soal tentang Logika Matematika. Dan juga, di Jurusan Teknik Informatika (TI) juga dipelajari kembali di Mata Kuliah Matematika Diskrit (Matdis).
Terima Kasih 😀😊😘👌👍 :)
Wassalamu‘alaikum Wr. Wb.






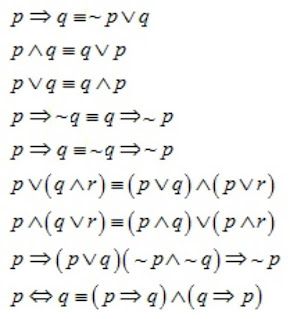




































Post a Comment