Materi Matdis Aljabar Boolean Lanjutan (Gerbang Logika dan Peta Karnaugh)

Assalamu‘alaikum Wr. Wb. 

Halo gais! Pada Postingan sebelumnya sudah membahas tentang Logika dan juga sedikit tentang Aljabar Boolean seperti Hukum-hukum, Bentuk Kanonik, hingga Tabel Kebenaran. Sekarang giliran membahas tentang Gerbang Logika dan Peta Karnaugh yang merupakan Lanjutan dari Aljabar Boolean untuk Mata Kuliah (Matkul) Matematika Diskrit (Matdis).

GERBANG LOGIKA

Sumber : Wikielektronika.com, Webstudi.site, Teknikelektronika.com, Gramedia.com, Dicoding.com, 

A. Pengertian dan Fungsi dari Gerbang Logika

Gerbang Logika atau Logic Gate adalah proses pengolahan input bilangan biner dengan teori Matematika Boolean. Seperti yang kita ketahui, bilangan biner sendiri terdiri dari angka 1 dan 0.

Logic Gate ini direpresentasikan menggunakan tabel kebenaran. Jika memiliki nilai benar (true) akan ditunjukan dengan angka “1”. Sebaliknya, jika memiliki nilai salah (false) akan ditunjukan dengan angka “0”.

Gerbang logika memiliki fungsi untuk melakukan fungsi logika dasar untuk membentuk sirkuit digital yang terintegrasi. Kebanyakan logic gate menggunakan bilangan biner 0 atau 1 bisa juga disebut true atau false. Biasanya terdiri dari dua buah nilai input dan satu nilai output.

B. Jenis-jenis Gerbang Logika

Terdapat beberapa jenis logic gate yang umum digunakan. Berikut adalah jenis-jenis gerbang logika dan tabel kebenarannya.

1. Gerbang AND

Jenis pertama adalah gerbang AND. Gerbang AND ini memerlukan dua atau lebih input untuk menghasilkan satu output. Jika semua atau salah satu inputnya merupakan bilangan biner 0, maka outputnya akan menjadi 0. Sedangkan jika semua input adalah bilangan biner 1, maka outputnya akan menjadi 1.

2. Gerbang OR

Jenis kedua adalah gerbang OR. Sama seperti gerbang sebelumnya, gerbang ini juga memerlukan dua input untuk menghasilkan satu output. Gerbang OR ini akan menghasilkan output 1 jika semua atau salah satu input merupakan bilangan biner 1. Sedangkan output akan menghasilkan 0 jika semua inputnya adalah bilangan biner 0.

3. Gerbang NOT

Jenis berikutnya adalah gerbang NOT. Gerbang NOT ini berfungsi sebagai pembalik keadaan. Jika input bernilai 1 maka outputnya akan bernilai 0 dan begitu juga sebaliknya.

4. Gerbang NAND

Selanjutnya adalah gerbang NAND. Gerbang NAND ini adalah gabungan dari gerbang AND dan gerbang NOT. Karena itu output yang dihasilkan dari gerbang NAND ini adalah kebalikan dari gerbang AND.

5. Gerbang NOR

Berikutnya adalah gerbang NOR. Gerbang NOR ini adalah gabungan dari gerbang OR dan gerbang NOT. Sehingga output yang dihasilkan dari gerbang NOR ini adalah kebalikan dari gerbang OR.

6. Gerbang XOR

Jenis berikutnya adalah gerbang XOR. Gerbang XOR ini memerlukan dua input untuk menghasilkan satu output. Jika input berbeda (misalkan: input A=1, input B=0) maka output yang dihasilkan adalah bilangan biner 1. Sedangkan jika input adalah sama maka akan menghasilkan output dengan bilangan biner 0.

7. Gerbang XNOR

Jenis yang terakhir adalah gerbang XNOR. Gerbang XNOR ini memerlukan dua input untuk menghasilkan satu output. Jika input berbeda (misalkan: input A=1, input B=0) maka output yang dihasilkan adalah bilangan biner 0. Sedangkan jika input adalah sama maka akan menghasilkan output dengan bilangan biner 1.

C. Contoh-contoh Gerbang Logika

Sumber : Webstudi.site

Berikut, inilah Contoh-contoh Soal dari Gerbang Logika.

1. Suatu gerbang AND dengan masukan A dan B diberi masukan grafik logika seperti Gambar berikut. Tentukan grafik keluaran z!

Jawaban :

Berdasar tabel kebenaran pada Gambar diatas, didapat bahwa masukan AND hanya akan berlogika 1 jika kedua masukan/input berlogika 1. Sehingga grafik keluaran/output Y seperti gambar berikut.

2. Gambarkan untai gerbang dan saklar untuk gerbang OR dan AND yang dinyatakan dengan persamaan Y = (A + B).C!

Jawaban :

Persamaan tersebut mengharuskan masukan A dan B di-OR-kan, hasilnya kemudian di-AND-kan dengan C.

3. Tiga buah gerbang NAND dirangkai seperti gambar dibawah. Buatlah tabel kebenaran untai tersebut!

Jawaban :

Tabel kebenaran harus memuat seluruh variasi masukan A, B, C dan D. Karena ada 4 masukan, maka jumlah variasi ada 24 = 16, sehingga tabel akan mempunyai 16 baris.

Tabel kebenaran tersebut dapat dibuat per baris maupun per kolom. Jika dibuat per baris, maka pada baris pertama tentukan kombinasi untuk A, B, C dan D. Logika E ditentukan dari kolom A dan B, E = A NAND B. Logika F ditentukan dari kolom C dan D, F = C NAND D. Sedangkan logika keluaran Y ditentukan dari kolom E dan F, Y = E NAND F. 

Sedangkan jika dibuat per baris kolom, maka tentukan dulu kombinasi masukan A, B, C dan D. Logika E, F dan Y dapat ditentukan dengan cara yang sama seperti di atas.

4. Berikut sebuah untai logika yang dibentuk dari gerbang AND dan OR.

Untuk dapat merealisasikan untai tersebut, dibutuhkan 2 buah IC digital. Pertama, IC yang mempunyai gerbang AND yaitu 7408. Kedua, IC yang mempunyai gerbang OR yaitu 7432. Gerbang pertama dan kedua menggunakan dua buah gerbang pada IC 7408, dan gerbang ketiga hanya menggunakan sebuah gerbang pada IC 7432. 

Dengan memanfaatkan sifat universal dari gerbang NAND, ubahlah untai di atas agar dapat direalisasikan menggunakan gerbang NAND saja! Berapa IC yang dibutuhkan ?

Jawaban :

Berdasar universalitas gerbang NAND dan NOR, gerbang AND dapat diwakili oleh dua buah gerbang NAND; sedangkan gerbang OR dapat diwakili oleh tiga buah gerbang NAND. Sehingga terbentuk 7 buah gerbang NAND seperti pada Gambar dibawah

Kita misalkan gerbang AND bagian atas diberi nomor 1 dan yang bawah diberi nomor 2, sedangkan gerbang OR di sebelah kanan diberi nomor 3. Gerbang nomor 1 dapat diganti dengan NAND menjadi gerbang nomor 1A dan 1B. Demikian pula gerbang nomor 2 dapat diganti menjadi gerbang nomor 2A dan 2B. Sedangkan gerbang nomor 3 yaitu OR dapat diganti dengan tiga gerbang NAND menjadi gerbang nomor 3A, 3B dan 3C.

Terdapat dua pasang NOT ganda, yaitu gerbang 1B-3A dan 2B-3B. Kedua pasang NOT tersebut dapat dihilangkan. Sehingga hasil akhir hanya dibentuk oleh tiga buah gerbang NAND. Untai hasil hanya menggunakan tiga gerbang NAND. Karena sebuah IC NAND 7400 mempunyai empat gerbang NAND, maka realisasi untai tersebut hanya membutuhkan sebuah IC.

Perhatikan bahwa untai pada dua Gambar diatas mempunyai fungsi logika sama. Silakan dicek dengan membuat tabel kebenaran untuk kedua untai tersebut dan bandingkan!

5. Salah satu contoh penerapan gerbang X-NOR adalah untai pendeteksi kesamaan dua bilangan biner sebagaimana Gambar di bawah. Tentukan kombinasi masukan x₁, x₀, y₁ dan y₀ yang akan menjadikan Z=1!

Jawaban :

Y akan berlogika 1 jika kedua keluaran XOR berlogika 1. Hal ini hanya dapat terjadi jika x1 = y1 dan x0 = y0. Lihat tabel kebeneran berikut.

Tabel kebenaran pada Contoh tersebut di atas merupakan tabel kebenaran yang menggunakan format diperpendek. Dengan empat masukan, seharusnya tabel kebenaran di atas mempunyai 16 baris. Namun karena empat variasi masukan yang menjadikan keluaran 1 merupakan jawaban atas pertanyaan, maka dapat saja hanya keempat variasi masukan tersebut yang ditampilkan. Variasi masukan lainnya boleh tidak ditampilkan dan cukup dituliskan kata ‘lainnya’.

6. Buatlah Tabel Kebenaran untuk fungsi logika pada titik C, D dan Q pada sirkuit berikut serta identifikasi gerbang logika tunggal yang dapat digunakan untuk mengganti seluruh rangkaian tersebut.

Jawaban :

Dari gambar rangkaian diatas dapat kita ketahui bawah terdapat 3 gerbang yaitu gerbang NAND 2-input, gerbang EX-OR 2-input dan terakhir gerbang EX-NOR 2-input pada bagian output. 

Karena hanya ada 2 input ke sirkuit A dan B, maka ada 4 kemungkinan kombinasi input (2²) yaitu : 0-0, 0-1, 1-0 dan 1-1. Berdasarkan kombinasi input tersebut maka akan dibuat tabel kebenaran seperti ini :

Dari tabel kebenaran di atas, kolom C mewakili fungsi keluaran yang dihasilkan oleh gerbang NAND, sedangkan kolom D mewakili fungsi keluaran dari gerbang Ex-OR. Dari kedua ekspresi output ini kemudian menjadi kondisi input untuk gerbang Ex-NOR.

Dapat dilihat dari tabel kebenaran bahwa output di Q akan bernilai 1 apabila salah satu dari dua input A atau B berada di logika 1. Satu-satunya tabel kebenaran yang memenuhi kondisi ini yaitu tabel kebenaran gerbang OR. Oleh karena itu, seluruh rangkaian di atas dapat diganti dengan gerbang OR 2 input.

7. Temukan ekspresi Aljabar Boolean untuk sistem berikut.

Jawaban :

Untuk sistem diatas terdiri dari Gerbang AND, Gerbang NOR dan Gerbang OR, ekspresi untuk gerbang AND adalah A.B, dan ekspresi untuk gerbang NOR adalah A+B. Dari kedua ekspresi ini juga memiliki input yang terpisah ke gerbang OR yang didefinisikan sebagai A+B. Jadi ekspresi keluaran akhir adalah sebagai berikut :

Output pada Q yaitu Q = (A.B)+(A+B), tetapi notasinya sama seperti notasi De'Morgan A.B maka notasi A.B diganti kedalam ekspresi output sehingga dihasilkan notasi ouput Q = (A.B)+(A.B), dimana merupakan  notasi Boolean untuk Gerbang Exclusive-NOR.

8. Temukan ekspresi Aljabar Boolean untuk sistem berikut

Jawaban :

Pada sistem rangkaian diatas mungkin terlihat lebih rumit daripada dua rangkaian sebelumnya. Jika dianalisa maka rangkaian logika diatas hanya terdiri dari gerbang dasar AND, OR dan NOT yang dihubungkan bersama.

Seperti contoh soal Aljabar Boolean sebelumnya, kita dapat menyederhanakan rangkaian sirkuit dengan menuliskan notasi Boolean pada setiap fungsi gerbang logika secara bergantian, agar didapatkan  ekspresi akhir untuk output pada Q.

Output dari gerbang AND 3-input yaitu logika "1" ketika semua input gerbang adalah "HIGH" pada level logika "1" (A.B.C). Output dari gerbang OR yang lebih rendah hanya "1" ketika satu atau kedua input B atau C berada pada level logika "0". 

Output dari gerbang AND 2-input adalah "1" ketika input A adalah "1" dan input B atau C berada pada "0". Maka output pada Q hanya “1” ketika input A.B.C sama dengan “1” atau A sama dengan “1” dan keduanya input B atau C sama dengan “0”, A.(B+C).

Dengan menggunakan "teorema de Morgan", input B dan input C dapat diputus untuk menghasilkan output pada Q, yang mana dapat berupa logika "1" atau pada logika "0". Maka satu-satunya input yaitu input A, sebagai satu-satunya input yang diperlukan untuk memberikan output pada Q seperti yang ditunjukkan pada tabel di bawah ini.

Berdasarkan rangkaian logika di atas maka dapat disimpulkan bawah input pada rangkaian tersebut dapat  diganti dengan hanya satu input tunggal yaitu input "A" sehingga akan mengurangi jumlah sirkutnya dengan hanya satu kawat, (atau Buffer). 

D. Operasi Aljabar Boolean dan Bentuk Kanonik (Contoh Implementasi Gerbang Logika) [Study Case]

Sumber : Webstudi.site dan Matkul.xyz

Untuk Aljabar Boolean dalam bentuk Kanonik sudah pernah dibahas di Postingan sebelumnya. Untuk melihat selengkapnya, silakan lihat di sini. Dan berikut inilah beberapa Contoh Soal terkait dengan Bentuk Kanonik dengan menggunakan Gerbang Logika.

Dalam suatu BANK terdapat beberapa Brangkas yang berisi uang, emas, dan dokumen-dokumen penting lainnya. dalam BANK tersebut terdapat beberapa direktur dan direktu. untuk dapat membuka brangkas tersebut minimal 2 orang baik direksi maupun direktur untuk dapat membuka bangkas tearsebut.   Dalam kasus tersebut, buatlah rangkaian logika sederhana agar kasus tersebut bisa berjalan.

Penyelesaian :

Gambar rangkaian logikanya :

PETA KARNAUGH

Sumber Materi : Adoc.pub (PDF) (Mulai Halaman 5), Djukarna.wordpress.com, Jati.ITDA.ac.id (Blogspot)

Karnaugh Map (Kmap) adalah diagram yang merepresentasikan table kebenaran menggunakan matriks persegi (cells), dimana setiap kotak persegi mewakili nilai minterm (maxterm) dari logic function. Kmap membantu menyederhanakan persamaan dari table kebenaran untuk rangkaian yang kompleks. Kmap memiliki beberapa kelebihan, diantaranya adalah lebih sederhana dalam proses penyederhanaannya untuk memperoleh jumlah literal yang lebih sedikit. 

Karnaugh Map Method (Metode Peta Karnaugh) adalah metode untuk menyederhanakan persamaan aljabar Boolean. Metode ini pertama kali diperkenalkan oleh Maurice Karnaugh pada Tahun 1953 yang merupakan penyederhanaan dari metode Veitch Chart (Kartu Veitch).

Apabila ada fungsi n-variabel, dibutuhkan 2ⁿ baris tabel kebenaran, dan pada Kmap dibutuhkan 2ⁿ kotak persegi. Nilai dari tabel kebenaran tersebut ditulis kembali di kotak persegi pada posisi yang mewakli posisinya di tabel kebenaran.

Langkah-langkah menyajikan fungsi ke dalam Kmap adalah :

• Buat diagram matriks sebanyak 2ⁿ kotak persegi, dimana n adalah jumlah variable fungsi.
• Setiap kotak-kotak persegi tersebut diisi sesuai dengan nilai yang diberikan dari fungsi atau nilai dari table kebenaran pada letak yang tepat. 

A. Penyajian Fungsi dalam Karnaugh Map

1. Penyajian Kmap 2-Variabel

Pada penyajian Kmap 2-variabel dibutuhkan 4 (2ⁿ) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada gambar di bawah Terdapat berbagai macam cara dalam menyusun matriks Kmap dan kita boleh memilih, dengan syarat tetap konsisten pada posisi dimana minterm berada.

Contoh Soal :

Tabel kebenaran dengan fungsi F = X.Y’+X.Y , seperti yang ditunjukkan pada Tabel dibawah Bentuk penyajiannya ke dalan Kmap seperti ditunjukkan pada Gambar di bawah.

2. Penyajian Kmap 3-Variabel

Pada penyajian Kmap 3-variabel dibutuhkan 8 (2³) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada Gambar di bawah.

Pada susunan matriks Kmap 3-varaibel ke atas, terdapat urutan matriks yang harus diperhatikan. Pada matriks Kmap, dari setelah m₁ (x’y’z) urutan selanjutnya adalah m₃ (x’.y.z), bukan m₂ (x’yz’). Begitu pula m₅ (xy’z) urutan selanjutnya adalah m₇ (xyz), bukan m₆ (xyz’). Hal ini terjadi, disebabkan pada aturan pengurutan Kmap, kotak yang bersebelahan haruslah hanya memiliki satu perubahan bit variable, dari 0 ke 1 atau dari 1 ke 0. Apabila urutan setelah m₁ (x’y’z) adalah m₂ (x’yz’), maka terdapat dua bit variable yang berubah yaitu y dan z. Bit variable y berubah dari y’ menjadi y dan bit variable z berubah dari z menjadi z’. Begitu pula yang terjadi pada m₅ (xy’z), apabila urutan setelah m₅ (xy’z) adalah m₆ (xyz’), maka terdapat dua bit variable yang berubah yaitu y dan z. Bit variable y berubah dari y’ menjadi y dan bit variable z berubah dari z menjadi z’.

Contoh Soal :

Cara penyajian Kmap dari table kebenaran. Bentuk penyajiannya ke dalan Kmap seperti ditunjukkan pada Gambar di bawah ini.

Cara penyajian Kmap dari fungsi minterm-nya, F(x,y,z) = Ʃm(2,3,4,5). Bentuk penyajiannya ke dalam Kmap seperti ditunjukkan pada Gambar di bawah.

Cara penyajian Kmap dari fungsi boolean-nya, F(A,B,C) = A’.C + A’.B + A.B’.C + B.C Bentuk penyajiannya ke dalam Kmap seperti ditunjukkan pada Gambar di bawah.

3. Penyajian Kmap 4-Variabel

Pada penyajian Kmap 4-variabel dibutuhkan 16 (2⁴) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada Gambar di bawah. 

4. Penyajian Kmap 5-Variabel

Pada penyajian Kmap 5-variabel dibutuhkan 32 (2⁵) kotak persegi untuk Kmap. Cara mengisi masing-masing kotak persegi pada Kmap ditunjukkan pada Gambar di bawah. 

Cara membuat fungsi hasil Kmap, seperti yang ditunjukkan pada Gambar di bawah, yaitu menulis fungsi-fungsi minterm (maxterm) dimana kotak pada Kmap bernilai 1 (0), kemudian menghubungkannya dengan sum atau OR. 

B. Minimization Karnaugh Map

Pada Kmap dikenal istilah Implicant dan Prime Implicant untuk membantu dalam menemukan fungsi yang paling sederhana atau mengandung sedikit mungkin jumlah variable dan jumah literal.

Implicant adalah angka 1 baik yang sendiri maupun yang telah dikelompokkan. Sedangkan, Prime Implicant adalah suatu pengelompokkan angka 1 pada kotak-kotak yang bersebelahan secara maksimal, dengan cara memaksimalkan jumlah kotak yang bersebelahan dalam satu kelmpok. Dengan kata lain kelompok yang mungkin yang dapat mengelompokkan angka 1 secara luas. Prime implicant harus dapat meng-cover semua angka 1, seperti yang ditunjukkan pada gambar 2.9 Jumlah kotak yang masuk dalam satu kelompok haruslah berjumlah 2ⁿ.

Penyajian dengan map Karnaugh

Semua yang dilingkari pada gambar diatas adalah prime implicant. Selanjutnya dikenal istilah prime implicant essential, yaitu prime implicant satu-satunya yang dapat mengelompokkan minterm (maxterm), selain itu dalam satu prime implicant hanya terdapat minimal satu minterm yang hanya dapat di-cover oleh prime implicant essential dan tidak di-cover oleh prime implicant yang lain. Penjelasan lebih lanjut tentang prime implicant essential dapat dilihat pada 2 gambar dibawah ini.

Penyederhanaan dengan map Karnaugh

Pada Kmap gambar diatas terdapat lebih dari satu kombinasi fungsi :

• F(A,B,C,D)  =  BC’  +  A’B’D  →  merupakan minimum dari Prime implicant, karena BC’ dan A’B’D merupakan prime implicant yang ESSENTIAL.
• F(A,B,C,D) =  BC’ + A’B’D + A’C’D  → benar tapi tidak minimum. A’C’D adalah prime implicant yang NON-ESSENTIAL karena angka 1-nya ada yang sudah dicover dengan Prime Implicant yang lain. 
• F(A,B,C,D) ≠   A’B’D + A’C’D  → keduanya memang Prime Implicant namun ada angka 1 yang belum tercover. 

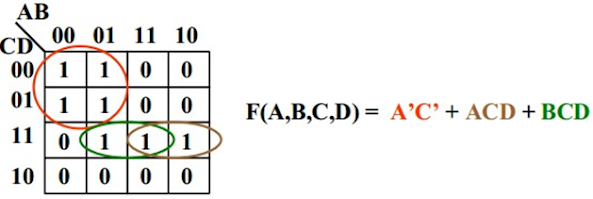
Pada gambar dibawah, A’.C’ dan ACD adalah Prime Implicant yang essential, sedangkan BCD adalah Prime Implicant yang non-essential. 

Penyederhanaan dengan map Karnaughprime implicant essential

Langkah-langkah untuk mendapatkan fungsi penyederhanaan dengan Kmap terdiri atas :

• Buat matriks Kmap sesuai dengan banyaknya variable.
• Kelompokkan beberapa kotak yang bernilai 1 jika fungsi minterm (bernilai 0 bila maxterm), dengan syarat beberapa kotak tersebut bersebelahan secara 4 arah mata angin dan depan belakang. Selain itu kotak-kotak yang dikelompokkan dalam satu kelompok harus berjumlah 2ⁿ (2,4,8, …).
• Tentukan Prime Implicant, dengan mengelompokkan kotak seluas mungkin yang bisa dikelompokkan. Karena semakin banyak kotak yang dikelompokkan dalam satu kelompok, semakin sedikit varibel yang dihasilkan.
• Tentukan Prime Implicant yang essential.
• Tentukan Prime Implicant tambahan, apabila dibutuhkan untuk meng-cover minterm (maxterm) sisa yang belum ter-cover Prime Implicant yang essential.

Contoh penyederhanaan Kmap 2-variabel ditunjukkan pada Gambar dibawah ini :

Maka dari fungsi hasil penyederhanaan adalah fungsi OR → Z = X + Y 

 

Contoh penyederhanaan Kmap 3-variabel ditunjukkan pada Gambar dibawah.

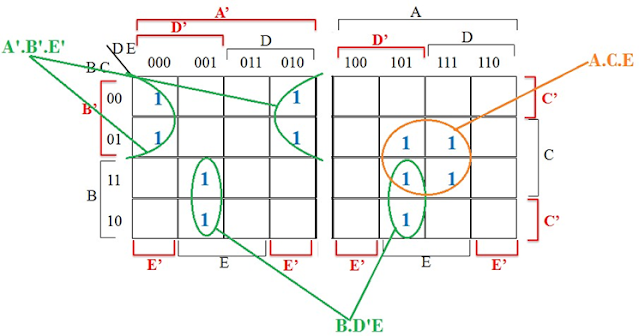
Contoh penyederhanaan Kmap 5-variabel ditunjukkan pada gambar dibawah, maka diperoleh fungsi F(A,B,C,D,E) = A’.B’.E’ + B.D’.E + A.C.E. 

 

 Pada penyederhanaan tidak diperbolehkan mengelompokkan kotak selain yang bersebelahan pada empat arah mata angin dan depan belakang, jika itu dilakukan maka kelompok tersebut akan disebut Illegal grouping. Contoh illegal grouping ditunjukkan pada 2 gambar dibawah. 

Penyederhanaan dengan map Karnaugh 5 variabel

Penyederhanaan dengan map Karnaugh illegal grouping

Penyederhanaan dengan menggunakan Kmap memiliki beberapa kelemahan, diantaranya : 

1. Ada lebih dari satu cara untuk mengelompokkan

Contoh : 

a. Pada fungsi f(A,B,C,D) = Ʃm (0,2,4,5,7,10,11,14,15) 

f(A,B,C,D) = A’B’D’ + A’BC’ +BCD +AC atau f(A,B,C,D) = A’C’D’ + A’BD + B’CD’ +AC 

b. Pada fungsi f(A,B,C,D) = Ʃm (0,1,2,3,4,6,8,10,12,13,14,15) 

2. Kmap hanya praktis untuk maksimum 4-variabel. Semakin banyak jumlah variable maka semakin banyak pula kotak yang dibutuhkan. Hal tersebut mgakibatkan semakin sulit untuk menentukan kotak mana yang bersebelahan. 

3. Adanya trial-and-error, dimana hal tersebut bergantung pada kemampuan pengguna dalam mengenali pola fungsi yang seharusnya.

VIDEO MATERI

Untuk memahami lebih lanjut terkait dengan Peta Karnaugh, lihatlah Video-video YouTube di bawah ini.

Dan untuk membaca Artikel sebelumnya tentang Aljabar Boolean, silakan lihat di sini. 

Nantikan juga Artikel/Materi Matematika Diskrit selanjutnya tentang Teori Graf dan Teori Tree. So, stay tuned!

Terima Kasih 😀😊😘👌👍 :)

Wassalamu‘alaikum Wr. Wb.