Materi Matematika Diskrit : Teori Tree (Tree Theory)

May 17, 2022

Assalamu‘alaikum Wr. Wb.

Halo guys! Jika sebelumnya sudah membahas tentang Teori Graf, pada Postingan ini kami akan memberikan Materi Terakhir untuk Mata Kuliah (Matkul) Matematika Diskrit (Matdis), yaitu Teori Tree (Tree Theory).

Sumber Materi : Academia.edu (PDF), Repository.Unikom.ac.id (PDF), Slideplayer.info (PPT), Tutorialspoint.com, Javatpoint.com, Geeksf orgeeks.org, dan Teknocrash.web.id

Pohon (Tree) merupakan salah satu bentuk khusus dari struktur suatu graf. Misalkan A merupakan sebuah himpunan berhingga simpul (vertex) pada suatu graf G yang terhubung. Untuk setiap pasangan simpul di A dapat ditentukan suatu lintasan yang menghubungkan pasangan simpul tersebut. Suatu graf terhubung yang setiap pasangan simpulnya hanya dapat dihubungkan oleh suatu lintasan tertentu, maka graf tersebut dinamakan pohon (tree). Dengan kata lain, pohon (tree) merupakan graf tak-berarah yang terhubung dan tidak memiliki sirkuit.

Contoh :

Hutan (forest) merupakan kumpulan pohon yang saling lepas. Dengan kata lain, hutan merupakan graf tidak terhubung yang tidak mengandung sirkuit. Setiap komponen di dalam graf terhubung tersebut adalah pohon. Pada Gambar diatas, G4 merupakan salah satu contoh hutan, yaitu hutan yang terdiri dari dua pohon.

Berikut adalah beberapa sifat pohon :

Misalkan G merupakan suatu graf dengan n buah simpul dan tepat n–1 buah sisi.
Jika G tidak mempunyai sirkuit maka G merupakan pohon.
Suatu pohon dengan n buah simpul mempunyai n–1 buah sisi.
Setiap pasang simpul di dalam suatu pohon terhubung dengan lintasan tunggal.
Misalkan G adalah graf sederhana dengan jumlah simpul n, jika G tidak mengandung sirkuit maka penambahan satu sisi pada graf hanya akan membuat satu sirkuit.

A. Pohon Merentang Minimum (Minimum Spanning Tree)

Spanning Tree dari suatu graf terhubung merupakan subgraf merentang yang berupa pohon. Pohon merentang diperoleh dengan cara menghilangkan sirkuit di dalam graf tersebut.

Contoh spanning tree dari suatu graf terhubung (Munir, 2003) :

Terlihat bahwa T₁, T₂, T₃, T₄ merupakan spanning tree dari graf G. Perlu diperhatikan bahwa setiap graf terhubung berbobot paling sedikit mempunyai satu buah spanning tree. Pohon rentang yang memiliki bobot minimum dinamakan pohon merentang minimum (minimum spanning tree). Dalam kehidupan nyata, salah satu contoh aplikasi spanning tree adalah menentukan rangkaian jalan dengan jarak total seminimum mungkin yang menghubungkan semua kota sehingga setiap kota tetap terhubung satu sama lain.

1. Algoritma Prim

Dalam menentukan suatu Minimum Spanning Tree dari suatu graf terhubung, kita dapat menentukannya dengan menggunakan 2 cara yaitu Algoritma Prim dan Algoritma Kruskal. Algoritma Prim memiliki langkah-langkah sebagai berikut :

Pilih sisi dari graf G yang berbobot minimum, masukkan ke dalam T.
Pilih sisi (u, v) dalam G yang mempunyai bobot minimum dan bersisian dengan simpul di T, dengan syarat sisi tersebut tidak membentuk sirkuit di T. Masukkan (u, v) ke dalam T.
Ulangi langkah 2 sebanyak n – 2 kali.

Jumlah langkah seluruhnya dalam algoritma Prim adalah sebanyak jumlah sisi di dalam spanning tree dengan n buah simpul, yaitu (n – 1) buah.

Contoh :

Tentukan Minimum Spanning Tree dari Graf dibawah ini :

Jawab :

Pilih sisi fg sehingga kita mempunyai T ({f, g}, fg)
Langkah selanjutnya dapat dipilih sisi ef karena sisi tersebut berbobot minimum yang bersisian dengan simpul f.
Selanjutnya pilih sisi ae atau gh karena sisi tersebut berbobot minimum yang bersisian dengan simpul pada T, yaitu e dan g.

Jika proses ini dilanjutkan terus maka akan diperoleh minimum spanning tree seperti dibawah ini :

Terlihat bahwa spanning tree tersebut mempunyai total bobot 2 + 3 + 4 + 4 + 4 + 4 + 3 = 24.

2. Algoritma Kruskal

Langkah-langkah dalam algoritma Kruskal agak berbeda dengan algoritma Prim. Pada Algoritma Kruskal, semua sisi dengan bobot yang minimal dimasukan kedalam T secara berurutan.

Langkah-langkah dalam menentukan minimum spanning tree dengan algoritma Kruskal adalah sebagai berikut :

Langkah 1 : T berbentuk seperti pohon berikut.

Langkah 2 : Memasukan sisi-sisi yang berbobot 3 kedalam sehingga T berbentuk.

Langkah 3 : Memasukan sisi-sisi yang berbobot 4 kedalam sehingga akhirnya diperoleh minimum spanning tree berikut.

B. Pohon Berakar

Pada suatu pohon, yang sisi-sisinya diberi arah sehingga menyerupai graf berarah, maka simpul yang terhubung dengan semua simpul pada pohon tersebut dinamakan akar. Suatu pohon yang satu buah simpulnya diperlakukan sebagai akar maka pohon tersebut dinamakan pohon berakar (rooted tree). Simpul yang berlaku sebagai akar mempunyai derajat masuk sama dengan nol. Sementara itu, simpul yang lain pada pohon itu memiliki derajat masuk sama dengan satu. Pada suatu pohon berakar, Simpul yang memiliki derajat keluar sama dengan nol dinamakan daun.

Contoh : Pohon Berakar (Munir, 2003)

Pada pohon berakar diatas :

a merupakan akar
c, d, f, g, h, i, dan j merupakan daun

Terminologi pada Pohon Berakar

Perhatikan pohon berakar berikut ini :

1. Anak (Child/Children) dan Orangtua (Parent)

b, c, dan d adalah anak-anak simpul a, a adalah orangtua dari anak-anak itu.

2. Lintasan (Path)

Lintasan dari a ke h adalah a, b, e, h. dengan panjang lintasannya adalah 3. f adalah saudara kandung e, tetapi, g bukan saudara kandung e, karena orangtua mereka berbeda.

3. Subtree

4. Derajat (Degree)

Derajat sebuah simpul adalah jumlah anak pada simpul tersebut.

Contoh :

Simpul yang berderajat 0 adalah simpul c, f, h, I, j, l, dan m.

Simpul yang berderajat 1 adalah simpul d dan g.

Simpul yang berderajat 2 adalah simpul b dan k.

Simpul yang berderajat 3 adalah simpul a dan e.

Jadi, derajat yang dimaksudkan di sini adalah derajat-keluar. Derajat maksimum dari semua simpul merupakan derajat pohon itu sendiri. Pohon di atas berderajat 3.

5. Daun (Leaf)

Simpul yang berderajat nol (atau tidak mempunyai anak) disebut daun. Simpul h, i, j, f,

c, l, dan m adalah daun.

6. Simpul Dalam (Internal Nodes)

Simpul yang mempunyai anak disebut simpul dalam. Simpul b, d, e, g, dan k adalah

simpul dalam.

7. Aras (Level) atau Tingkat

8. Tinggi (Height) atau Kedalaman (Depth)

Aras maksimum dari suatu pohon disebut tinggi atau kedalaman pohon tersebut.

Pohon di atas mempunyai tinggi 4.

Pohon berakar yang urutan anak-anaknya penting (diperhatikan) maka pohon

yang demikian dinamakan pohon terurut (ordered tree). Sedangkan, pohon berakar yang

setiap simpul cabangnya mempunyai paling banyak n buah anak disebut pohon n-ary.

Jika n = 2, pohonnya disebut pohon biner (binary tree).

C. Penelusuran Pohon Biner

Sebuah pohon biner T dapat didefinisikan sebagai sekumpulan terbatas dari elemen-elemen yang disebut node/simpul dimana :

T dikatakan kosong (disebut NULL Tree/pohon NULL atau empty tree/pohon kosong)
T terdiri dari sebuah node khusus yang dipanggil R, disebut root dari T dan node-node.

T lainnya membentuk sebuah pasangan terurut dari binary tree T1 dan T2 yang tidak berhubungan yang kemudian dipanggil subtree kiri dan subtree kanan.

Jika T1 tidak kosong maka rootnya disebut successor kiri dari R dan jika T2 tidak kosong, maka rootnya disebut successor dari R.

1. Terminologi Binary Tree

R adalah sebuah simpul pada T dengan successor kiri S1, dan successor kanan S₂, maka R disebut parent dari S₁ dan S₂. S₁ disebut anak kiri (left child) dari R, dan S₂ adalah anak kanan (right child) dari R. S₁ dan S₂ dikatakan sibling (bersaudara). Derajat tertinggi dari sebuah simpul binary tree adalah 2.

Banyaknya simpul maksimum pada tingkat/level N adalah 2 ^(N-1), sehingga maksimum simpul sampai tingkat ke-N adalah :

sehingga jika binary tree lengkap bertingkat 5 maka banyaknya simpul adalah 25-1 = 31,

terdiri dari 16 leaf (daun) dan banyaknya simpul yang bukan daun termasuk akar adalah 15.

Jenis-Jenis Binary Tree.

Sehingga jika binary tree lengkap bertingkat 5 maka banyaknya simpul adalah 2⁵-1 = 31, terdiri dari 16 leaf (daun) dan banyaknya simpul yang bukan daun termasuk akar adalah 15.

Adapun Jenis-Jenis Binary Tree adalah sebagai berikut :

a. Complete Binary Tree

Suatu binary tree T akan disebut complete/lengkap jika semua levelnya memiliki child 2 buah kecuali untuk level paling akhir. Tetapi pada akhir level setiap leaf/daun muncul terurut dari sebelah kiri, seperti terlihat pada Gambar di bawah ini.

Sebuah binary tree yang lengkap dapat diberi label dengan sebuah bilangan bulat dari posisi kiri ke kanan. Dengan pemberian label ini, seseorang dapat dengan mudah menentukan child dan parent dari sebuah node/simpul K dalam sebuah complete tree T_n. Khususnya, left child (anak kiri) dari simpul K dapat diketahui dengan rumus 2K, dan right child (anak kanan) dari simpul K dapat diketahui dengan rumus 2K+1. Perhatikan di gambar bahwa simpul 5 mempunyai anak 10 (dari 2 ∙ 5) dan 11 (dari 2 ∙ 5 + 1). Sedangkan untuk mencari parent, rumusnya adalah K / 2 sehingga ketika simpul 6 yang diperiksa, itu berarti bahwa parent dari simpul 6 adalah 6 / 2 = 3.

b. Extended Binary Tree : 2-Tree

Sebuah binary tree dikatakan 2-tree atau extended binary tree jika tiap simpul N memiliki 0 atau 2 anak. Simpul dengan 2 anak disebut dengan simpul internal (internal node), dan simpul dengan 0 anak disebut dengan external node. Kadang-kadang dalam diagram node node tersebut dibedakan dengan menggunakan tanda lingkaran untuk internal node dan kotak untuk eksternal node.

Contoh :

2. Pembuatan Binary Tree

Pembuatan binary tree lebih mudah menggunakan binary search tree (binary sorted tree) dengan cara : “ Jika nilai dari simpul yang akan disisipkan lebih besar dari simpul parent, maka simpul tersebut ditempatkan sebagai subtree kanan. Jika lebih kecil maka simpul baru tersebut disimpan sebagai subtree kiri”.

Contoh :

Tree yang akan dibuat adalah : HAKCBLJ
H dijadikan sebagai root
A < H : A menjadi subtree kiri H
K > H : K menjadi subtree kanan H
C < H → C > A : C menjadi subtree kanan dari A.
B < H → B > A → B < C : B menjadi subtree kiri dari C.
L > H → L > K : L menjadi subtree kanan dari K.
J < H → J < K : J menjadi subtree kiri dari K.

3. Penelusuran Pohon Biner (Traversing Binary Tree)

Ada 3 (Tiga) cara yang standar untuk menelususi sebuah Binary Tree yaitu :

a. Preorder (Node – Left – Right [NLR])

Proses root
Telusuri subtree kiri (Left) secara preorder
Telusuri subtree kanan (Right) secara preorder

b. Inorder (Left – Node – Right [LNR])

Telusuri subtree kiri (Left) secara inorder
Proses root
Telusuri subtree kanan (Right) secara inorder

c. Postorder (Left – Right – Node [LNR])

Telusuri subtree kiri (Left) secara postorder
Telusuri subtree kanan (Right) secara postorder
Proses root

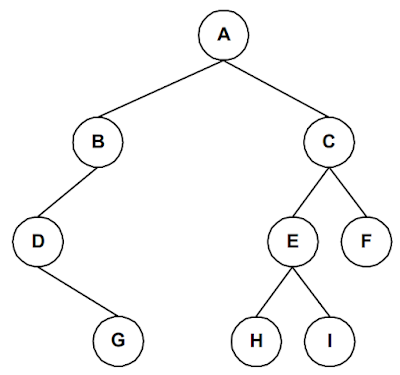
Contoh :

Secara Preorder : ABDGCEHIF
Secara Inorder : DGBAHEICF
Secara Postorder : GDBHIEFCA

4. Penerapan Binary Tree dalam Pemrograman

Tidak seperti struktur data linier (Array, Linked List, Queues, Stacks, dll) yang hanya memiliki satu cara logis untuk melintasinya, pohon dapat dilintasi dengan cara yang berbeda. Berikut ini adalah cara yang umum digunakan untuk melintasi pohon.

a. Inorder Traversal

Algorithm Inorder(tree)
   1. Traverse the left subtree, i.e., call Inorder(left-subtree)
   2. Visit the root.
   3. Traverse the right subtree, i.e., call Inorder(right-subtree)

b. Preorder Traversal

Algorithm Preorder(tree)
   1. Visit the root.
   2. Traverse the left subtree, i.e., call Preorder(left-subtree)
   3. Traverse the right subtree, i.e., call Preorder(right-subtree)

c. Postorder Traversal

Algorithm Postorder(tree)
   1. Traverse the left subtree, i.e., call Postorder(left-subtree)
   2. Traverse the right subtree, i.e., call Postorder(right-subtree)
   3. Visit the root.

Contoh :

Contoh Program untuk Traversal Preorder, Inorder, dan Postorder untuk gambar yang diberikan di atas adalah 4 5 2 3 1.

a. Dalam Bahasa C

#include <stdio.h>
#include <stdlib.h>
 
/* A binary tree node has data, pointer to left child
   and a pointer to right child */
struct node {
    int data;
    struct node* left;
    struct node* right;
};
 
/* Helper function that allocates a new node with the
   given data and NULL left and right pointers. */
struct node* newNode(int data)
{
    struct node* node
        = (struct node*)malloc(sizeof(struct node));
    node->data = data;
    node->left = NULL;
    node->right = NULL;
 
    return (node);
}
 
/* Given a binary tree, print its nodes according to the
  "bottom-up" postorder traversal. */
void printPostorder(struct node* node)
{
    if (node == NULL)
        return;
 
    // first recur on left subtree
    printPostorder(node->left);
 
    // then recur on right subtree
    printPostorder(node->right);
 
    // now deal with the node
    printf("%d ", node->data);
}
 
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct node* node)
{
    if (node == NULL)
        return;
 
    /* first recur on left child */
    printInorder(node->left);
 
    /* then print the data of node */
    printf("%d ", node->data);
 
    /* now recur on right child */
    printInorder(node->right);
}
 
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct node* node)
{
    if (node == NULL)
        return;
 
    /* first print data of node */
    printf("%d ", node->data);
 
    /* then recur on left subtree */
    printPreorder(node->left);
 
    /* now recur on right subtree */
    printPreorder(node->right);
}
 
/* Driver program to test above functions*/
int main()
{
    struct node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
 
    printf("\nPreorder traversal dari binary tree adalah : \n");
    printPreorder(root);
 
    printf("\nInorder traversal dari binary tree adalah : \n");
    printInorder(root);
 
    printf("\nPostorder traversal dari binary tree adalah : \n");
    printPostorder(root);
 
    getchar();
    return 0;
}

b. Dalam Bahasa C++

#include <iostream>
using namespace std;
 
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node {
    int data;
    struct Node *left, *right;
};
 
//Utility function to create a new tree node
Node* newNode(int data)
{
    Node* temp = new Node;
    temp->data = data;
    temp->left = temp->right = NULL;
    return temp;
}
 
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    // first recur on left subtree
    printPostorder(node->left);
 
    // then recur on right subtree
    printPostorder(node->right);
 
    // now deal with the node
    cout << node->data << " ";
}
 
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    /* first recur on left child */
    printInorder(node->left);
 
    /* then print the data of node */
    cout << node->data << " ";
 
    /* now recur on right child */
    printInorder(node->right);
}
 
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    /* first print data of node */
    cout << node->data << " ";
 
    /* then recur on left subtree */
    printPreorder(node->left);
 
    /* now recur on right subtree */
    printPreorder(node->right);
}
 
/* Driver program to test above functions*/
int main()
{
    struct Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
 
    cout << "\nPreorder traversal dari binary tree adalah : \n";
    printPreorder(root);
 
    cout << "\nInorder traversal dari binary tree adalah : \n";
    printInorder(root);
 
    cout << "\nPostorder traversal dari binary tree adalah : \n";
    printPostorder(root);
 
    return 0;
}

c. Dalam Bahasa C#

using System;
 
/* Class containing left and
right child of current
node and key value*/
class Node {
    public int key;
    public Node left, right;
 
    public Node(int item)
    {
        key = item;
        left = right = null;
    }
}
 
class BinaryTree {
    // Root of Binary Tree
    Node root;
 
    BinaryTree() { root = null; }
 
    /* Given a binary tree, print
       its nodes according to the
       "bottom-up" postorder traversal. */
    void printPostorder(Node node)
    {
        if (node == null)
            return;
 
        // first recur on left subtree
        printPostorder(node.left);
 
        // then recur on right subtree
        printPostorder(node.right);
 
        // now deal with the node
        Console.Write(node.key + " ");
    }
 
    /* Given a binary tree, print
       its nodes in inorder*/
    void printInorder(Node node)
    {
        if (node == null)
            return;
 
        /* first recur on left child */
        printInorder(node.left);
 
        /* then print the data of node */
        Console.Write(node.key + " ");
 
        /* now recur on right child */
        printInorder(node.right);
    }
 
    /* Given a binary tree, print
       its nodes in preorder*/
    void printPreorder(Node node)
    {
        if (node == null)
            return;
 
        /* first print data of node */
        Console.Write(node.key + " ");
 
        /* then recur on left subtree */
        printPreorder(node.left);
 
        /* now recur on right subtree */
        printPreorder(node.right);
    }
 
    // Wrappers over above recursive functions
    void printPostorder() { printPostorder(root); }
    void printInorder() { printInorder(root); }
    void printPreorder() { printPreorder(root); }
 
    // Driver Code
    static public void Main(String[] args)
    {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
 
        Console.WriteLine("Preorder traversal "
                          + "dari binary tree adalah : ");
        tree.printPreorder();
 
        Console.WriteLine("\nInorder traversal "
                          + "dari binary tree adalah : ");
        tree.printInorder();
 
        Console.WriteLine("\nPostorder traversal "
                          + "dari binary tree adalah : ");
        tree.printPostorder();
    }
}

d. Dalam Bahasa Java

class Node {
    int key;
    Node left, right;
 
    public Node(int item)
    {
        key = item;
        left = right = null;
    }
}
 
class BinaryTree {
    // Root of Binary Tree
    Node root;
 
    BinaryTree() { root = null; }
 
    /* Given a binary tree, print its nodes according to the
      "bottom-up" postorder traversal. */
    void printPostorder(Node node)
    {
        if (node == null)
            return;
 
        // first recur on left subtree
        printPostorder(node.left);
 
        // then recur on right subtree
        printPostorder(node.right);
 
        // now deal with the node
        System.out.print(node.key + " ");
    }
 
    /* Given a binary tree, print its nodes in inorder*/
    void printInorder(Node node)
    {
        if (node == null)
            return;
 
        /* first recur on left child */
        printInorder(node.left);
 
        /* then print the data of node */
        System.out.print(node.key + " ");
 
        /* now recur on right child */
        printInorder(node.right);
    }
 
    /* Given a binary tree, print its nodes in preorder*/
    void printPreorder(Node node)
    {
        if (node == null)
            return;
 
        /* first print data of node */
        System.out.print(node.key + " ");
 
        /* then recur on left subtree */
        printPreorder(node.left);
 
        /* now recur on right subtree */
        printPreorder(node.right);
    }
 
    // Wrappers over above recursive functions
    void printPostorder() { printPostorder(root); }
    void printInorder() { printInorder(root); }
    void printPreorder() { printPreorder(root); }
 
    // Driver method
    public static void main(String[] args)
    {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
 
        System.out.println(
            "Preorder traversal dari binary tree adalah : ");
        tree.printPreorder();
 
        System.out.println(
            "\nInorder traversal dari binary tree adalah : ");
        tree.printInorder();
 
        System.out.println(
            "\nPostorder traversal dari binary tree adalah : ");
        tree.printPostorder();
    }
}

e. Dalam Bahasa Javascript

<script>
// javascript program for different tree traversals
 
/* Class containing left and right child of current
   node and key value*/
class Node {
    constructor(val) {
        this.key = val;
        this.left = null;
        this.right = null;
    }
}
 
    // Root of Binary Tree
    var root = null;

    /*
     * Given a binary tree, print its nodes according to the "bottom-up" postorder
     * traversal.
     */
    function printPostorder(node) {
        if (node == null)
            return;
 
        // first recur on left subtree
        printPostorder(node.left);
 
        // then recur on right subtree
        printPostorder(node.right);
 
        // now deal with the node
        document.write(node.key + " ");
    }
 
    /* Given a binary tree, print its nodes in inorder */
    function printInorder(node) {
        if (node == null)
            return;
 
        /* first recur on left child */
        printInorder(node.left);
 
        /* then print the data of node */
        document.write(node.key + " ");
 
        /* now recur on right child */
        printInorder(node.right);
    }
 
    /* Given a binary tree, print its nodes in preorder */
    function printPreorder(node) {
        if (node == null)
            return;
 
        /* first print data of node */
        document.write(node.key + " ");
 
        /* then recur on left subtree */
        printPreorder(node.left);
 
        /* now recur on right subtree */
        printPreorder(node.right);
        
    }

    // Driver method
     
        root = new Node(1);
        root.left = new Node(2);
        root.right = new Node(3);
        root.left.left = new Node(4);
        root.left.right = new Node(5);
 
        document.write("Preorder traversal dari binary tree adalah : <br/>");
        printPreorder(root);
 
        document.write("<br/>Inorder traversal dari binary tree adalah : <br/>");
        printInorder(root);
 
        document.write("<br/>Postorder traversal dari binary tree adalah : <br/>");
        printPostorder(root);
 
// This code is contributed by aashish1995
</script>

f. Dalam Bahasa Python

# A class that represents an individual node in a
# Binary Tree

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key

# A function to do inorder tree traversal
def printInorder(root):
 
    if root:
 
        # First recur on left child
        printInorder(root.left)
 
        # then print the data of node
        print(root.val),
 
        # now recur on right child
        printInorder(root.right)

# A function to do postorder tree traversal
def printPostorder(root):
 
    if root:
 
        # First recur on left child
        printPostorder(root.left)
 
        # the recur on right child
        printPostorder(root.right)
 
        # now print the data of node
        print(root.val),

# A function to do preorder tree traversal
def printPreorder(root):
 
    if root:
 
        # First print the data of node
        print(root.val),
 
        # Then recur on left child
        printPreorder(root.left)
 
        # Finally recur on right child
        printPreorder(root.right)

# Driver code
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print ("Preorder traversal dari binary tree adalah :")
printPreorder(root)
 
print ("\nInorder traversal dari binary tree adalah :")
printInorder(root)
 
print ("\nPostorder traversal dari binary tree adalah :")
printPostorder(root)

g. Hasil Output

Preorder traversal dari binary tree adalah :
1 2 4 5 3

Inorder traversal dari binary tree adalah :
4 2 5 1 3

Postorder traversal dari binary tree adalah :
4 5 2 3 1

Untuk Materi tentang Teori Tree ini ada sedikit menyangkut ke Algoritma dan Struktur Data. Untuk membaca Artikel sebelumnya tentang Linked List, silakan lihat di sini.

Dan mohon maaf apabila ada kesalahan sedikitpun. Terima Kasih 😀😊😘👌👍 :)

Wassalamu‘alaikum Wr. Wb.

Inzaghi's Blog (Legacy)

Materi Matematika Diskrit : Teori Tree (Tree Theory)

Ads