Assalamu‘alaikum Wr. Wb.
Hello guys! Apakah selama ini Anda merasa kesulitan dalam mengerjakan Soal-soal Matematika? Biasanya ada banyak Solusi/Penyelesaian dalam mengerjakannya, salah satunya dengan menggunakan Kalkulator. Namun, ada Mesin Pencarian yang bisa untuk memecahkan Rumus Matematika, yaitu Wolfram Alpha. Dan sejak pertengahan Tahun lalu (Juli 2021), kini telah tersedia Math Input di Wolfram|Alpha. Tujuannya agar memudahkan Pengguna (User) untuk memasukkan (Input) Rumus Matematika. Untuk Cara Kerjanya, mari kita simak pembahasannya pada Artikel ini (Tentang Matematika Dasar, Aljabar, dan Fungsi).
Sumber Utama : Wikipedia.org (Sebagian), Wolframalpha.com (Math Input), dan Wolfram.com (Blog) [Lalu diterjemahkan melalui Google Translate]
Sumber Rumus-rumus : Wolfram|Alpha Math, Microsoft Math Solver, dan Symbolab.com
Wolfram|Alpha adalah mesin penjawab yang dikembangkan oleh Wolfram Research. Merupakan layanan daring yang dapat menjawab pertanyaan-pertanyaan yang diberikan secara faktual dengan menghitung jawaban secara terstruktur. Wolfram Alpha memanfaatkan basis data terstruktur yang dimilikinya dan kemudian diolah dengan peranti lunak. Bila mesin pencari lain hanya dapat menampilkan informasi yang tersedia bebas di web, Wolfram Alpha memanfaatkan kumpulan data yang sudah dilisensi dan dinilai para pakar serta informasi luring. Wolfram Alpha dirilis ke publik pada 15 Mei 2009 (23 Jumadil Awal 1430 H) oleh Stephen Wolfram.
MATH INPUT DI WOLFRAM|ALPHA
Fitur ini dapat memeriksa Pekerjaan Rumah (PR) Matematika Anda menjadi lebih mudah. Gratis untuk semua orang, fitur ini memungkinkan pengguna menggunakan notasi buku teks untuk memasukkan Input Matematika dan melihatnya ditampilkan dalam 2D. Kami telah menyediakan template populer untuk Anda gunakan, karena Visualisasi yang lebih baik dan pengeditan cepat berarti hasil yang lebih cepat.
A. Fitur-fitur Input Matematika (Math Input)
1. Gunakan Templat yang disediakan untuk Anda agar mudah dimasukkan
Hemat waktu memasukkan masalah Anda dengan menggunakan template untuk notasi matematika yang paling umum. Kami memiliki template yang mencakup Matematika Dasar, Kalkulus dan Jumlah (Sum), Vektor dan Matriks, Trigonometri, dan banyak lagi.
2. Transformasi Otomatis (Autotransformations)
Anda juga dapat menghemat waktu dalam mode Input Matematika dengan mengandalkan transformasi otomatis. Cukup ketik "/" untuk melihat pecahan atau "^" untuk mendapatkan pangkat.
3. Bahasa Wolfram (Wolfram Language)
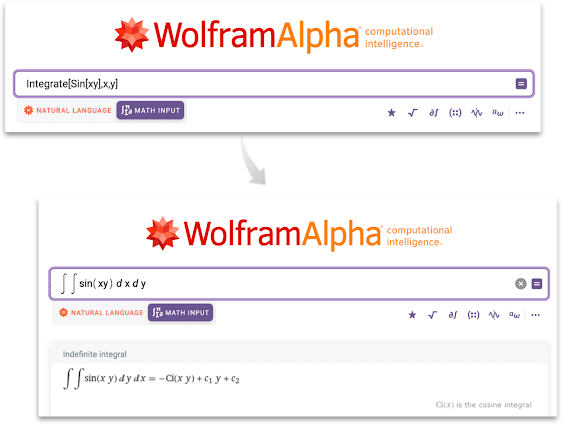
Pengguna Bahasa Wolfram akan menghargai bahwa Anda juga dapat memasukkan input Anda menggunakan Bahasa Wolfram. Jika ada template yang sesuai, input akan diubah menjadi input 2D untuk Anda. Coba ketik “Integrate[Sin[xy],x,y]” untuk melihatnya.
B. Cara Menggunakan Input Matematika di Wolfram|Alpha
1. Pilih Input Matematika
Sekarang ada tab Input Matematika di bawah bidang input yang memungkinkan pengguna untuk memasuki mode Input Matematika baru.
2. Masukkan Input Anda
Setelah dalam mode Input Matematika, pilih template dan isi. Kami telah menyediakan simbol untuk Anda untuk item seperti dan . Anda dapat menggunakan panah keyboard atau tombol Tab untuk menavigasi template untuk memasukkan input Anda. Pada perangkat sentuh, kami telah menyediakan panah untuk membantu navigasi.
3. Gunakan pencocokan braket dan sorotan templat untuk mengisi templat Anda dengan benar
Kami telah menambahkan fitur seperti menampilkan tanda kurung yang tidak cocok secara visual dan menyorot area masukan template saat Anda mengetik untuk mempermudah melihat masukan Anda.
4. Dapatkan hasil termasuk solusi langkah demi langkah
Setelah Anda memasukkan input, dapatkan jawaban Anda seperti biasa. Pengguna pro juga dapat melihat solusi langkah demi langkah untuk masalah yang dimasukkan dengan Input Matematika.
CONTOH INPUT MATEMATIKA DI WOLFRAM ALPHA
Dan berikut, inilah Contoh-contoh Inputan Rumus Matematika di Wolfram|Alpha dari yang Sederhana hingga yang tersulit.
A. Matematika Dasar
Matematika Dasar disini bisa berupa Perpangkatan/Eksponensial (Exponentiation), Perakaran (Roots), dan Pecahan (Fractions).
1. Pecahan (Fractions)
1/2
Wolfram Language :
Divide[1,2]
Alternate :
1/2
Math Input :
Klik di sini13/8
Wolfram Language :
Divide[13,8]
Alternate :
13/8
Math Input :
Klik di sini2+4/5
Wolfram Language :
2+Divide[4,5]
Alternate :
2 4/5 or 2+4/5
Math Input :
Klik di sini1/6+5/12+3/4
Wolfram Language :
Divide[1,6]+Divide[5,12]+Divide[3,4]
Alternate :
1/6+5/12+3/4
Math Input :
Klik di sini135/216-12/25
Wolfram Language :
Divide[135,216]+Divide[12,25]
Alternate :
135/216-12/25
Math Input :
Klik di sini4/9*2/5
Wolfram Language :
Divide[4,9]*Divide[2,5]
Alternate :
4/9*2/5
Math Input :
Klik di sini18/11:3/5
Wolfram Language :
Divide[18,11]:Divide[3,5]
Alternate :
18/11:3/5
Math Input :
Klik di sini(11/15)/(29/70)
Wolfram Language :
Divide[Divide[11,15],Divide[29,70]]
Alternate :
(11/15)/(29/70)
Math Input :
Klik di sini1/4*(4/3-1/2)
Wolfram Language :
Divide[1,4]*(Divide[4,3]+Divide[1,2])
Alternate :
1/4*(4/3-1/2)
Math Input :
Klik di sini(1-1/3+1/5)/(1/2-1/4+1/6)
Wolfram Language :
Divide[1-Divide[1,3]+Divide[1,5],Divide[1,2]-Divide[1,4]+Divide[1,6]]
Alternate :
(1-1/3+1/5)/(1/2-1/4+1/6)
Math Input :
Klik di sini2+1/(1+2/(3+1/5))
Wolfram Language :
2+Divide[1,1+Divide[2,3+Divide[1,5]]]
Alternate :
2+1/(1+2/(3+1/5))
Math Input :
Klik di sini2. Perpangkatan (Eksponensial)
2^5
Wolfram Language :
Power[2,5]
Alternate :
2^5
Math Input :
Klik di sini1.5^3
Wolfram Language :
Power[1.5,3]
Alternate :
1.5^3
Math Input :
Klik di sini3^4.5
Wolfram Language :
Power[3,4.5]
Alternate :
3^4.5
Math Input :
Klik di siniπ^e
Wolfram Language :
Power[π,e]
Alternate :
π^e
Math Input :
Klik di sini2^2+3
Wolfram Language :
Power[2,2]+3
Alternate :
2^2+3
Math Input :
Klik di sini3^5+4^2
(π+e)^3
2^(π-e)
Wolfram Language :
Power[2,π-e]
Alternate :
2^(π-e)
Math Input :
Klik di sini4^2*4^3
Wolfram Language :
Power[4,2]*Power[4,3]
Alternate :
4^2*4^3
Math Input :
Klik di sini(5^2)^3
Wolfram Language :
Power[(Power[5,2]),3]
Alternate :
(5^2)^3
Math Input :
Klik di sini4^3^2
Wolfram Language :
Power[4,Power[3,2]]
Alternate :
4^3^2 or 4^(3^2)
Math Input :
Klik di sini(3^8)/(3^5)
Wolfram Language :
Divide[Power[3,8],Power[3,5]]
Alternate :
(3^8)/(3^5)
Math Input :
Klik di sini3. Perakaran (Roots)
sqrt(9)
sqrt(50)
Wolfram Language :
Sqrt[50]
Alternate :
sqrt(50) or √50
Math Input :
Klik di sini4sqrt(3)
Wolfram Language :
4Sqrt[3]
Alternate :
4sqrt(3) or 4√3
Math Input :
Klik di sinicbrt(10)
Wolfram Language :
Cbrt[10]
Alternate :
cbrt(10)
Math Input :
Klik di siniroot(512,4)
Wolfram Language :
Surd[512,4] or Root[512,4]
Alternate :
root(512,4) or surd(512,4)
Math Input :
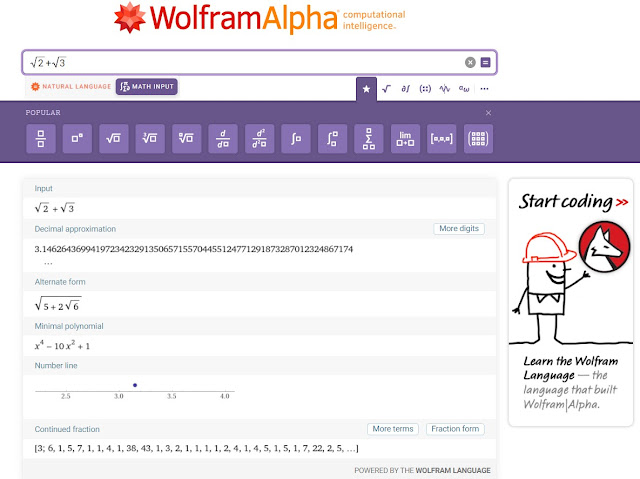
Klik di sinisqrt(2)+sqrt(3)
Wolfram Language :
Sqrt[2]+Sqrt[3]
Alternate :
sqrt(2)+sqrt(3) or √2+√3
Math Input :
Klik di sinisqrt(13)-sqrt(7)
Wolfram Language :
Sqrt[13]-Sqrt[7]
Alternate :
sqrt(13)-sqrt(7) or √13-√7
Math Input :
Klik di sinisqrt(15)-2sqrt(3)+3sqrt(2)
Wolfram Language :
sqrt[15]-2sqrt[3]+3sqrt[2]
Alternate :
sqrt(15)-2sqrt(3)+3sqrt(2) or √15-2√3+3√2
Math Input :
Klik di sinicbrt(15)+sqrt(60)-root(64,5)
Wolfram Language :
Cbrt[15]+Sqrt[60]-Surd[64,5]
Alternate :
cbrt(15)+sqrt(60)-root(64,5)
Math Input :
Klik di sinisqrt(9-4sqrt(5))
Wolfram Language :
Sqrt[9-4Sqrt[5]]
Alternate :
sqrt(9-4sqrt(5)) or √(9-4√5)
Math Input :
Klik di sinicbrt(2+root(15,4))
Wolfram Language :
Cbrt[2+Surd[15,4]]
Alternate :
cbrt(2+root(15,4))
Math Input :
Klik di sini(sqrt(2)+sqrt(5))/(sqrt(10)-sqrt(7))
Wolfram Language :
Divide[(Sqrt[2]+Sqrt[5]),(Sqrt[10]-Sqrt[7])]
Alternate :
(sqrt(2)+sqrt(5))/(sqrt(10)-sqrt(7)) or (√2+√5)/(√10-√7)
Math Input :
Klik di sini(sqrt(10)-sqrt(5))/(cbrt(15)+cbrt(21))
Wolfram Language :
Divide[(Sqrt[10]-Sqrt[5]),(Cbrt[15]+Cbrt[21])]
Alternate :
(sqrt(10)-sqrt(5))/(cbrt(15)+cbrt(21))
Math Input :
Klik di siniB. Aljabar
Aljabar disini bisa berupa Aljabar Dasar (Penyederhanaan Pangkat), Persamaan, dan Pertidaksamaan.
1. Aljabar Sederhana
ab+cb
Wolfram Language and Alternate :
ab+cb
Math Input :
Klik di sini2x-3y+7x+4+x-y
Wolfram Language and Alternate :
2x-3y+7x+4+x-y
Math Input :
Klik di sinia(b+c)
(x+a)(y+b)
x(x+2)
(2p+3)^2
Wolfram Language :
Power[(2p+3),2]
Alternate :
(2p+3)^2
Math Input :
Klik di sini
(x-4)/5+(3-x)/2
Wolfram Language :
Divide[x-4,5]+Divide[3-x,2]
Alternate :
(x-4)/5+(3-x)/2
Math Input :
Klik di sinix/2y+2x/y
Wolfram Language :
Divide[x,2y]+Divide[2x,y]
Alternate :
x/2y+2x/y
Math Input :
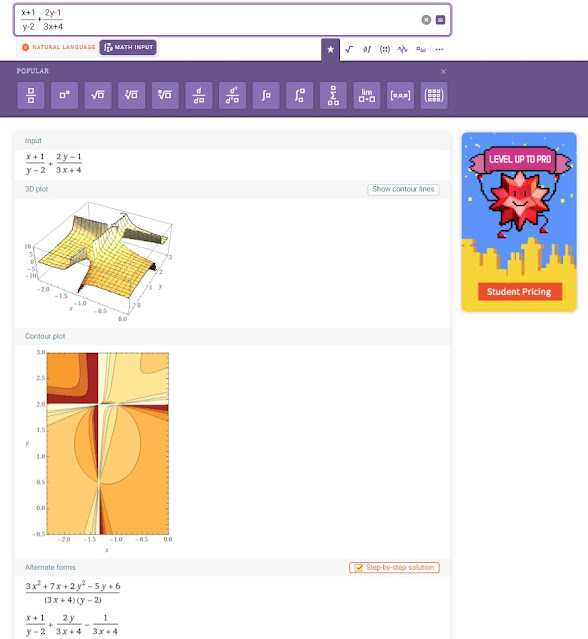
Klik di sini(x+1)/(y-2)+(2y-1)/(3x+4)
Wolfram Language :
Divide[x+1,y-2]+Divide[2y-1,3x+4]
Alternate :
(x+1)/(y-2)+(2y-1)/(3x+4)
Math Input :
Klik di sini2. Aljabar Eksponensial & Akar
(x^2*y^4)*(x^3*y)
Wolfram Language :
Power[x,2]Power[y,4]*Power[x,3]y
Alternate :
x^2y^4*x^3y or (x^2*y^4)*(x^3*y)
Math Input :
Klik di sini(a^2)/(4ab)+(2b)/(3ab)
Wolfram Language :
Divide[Power[a,2],4ab]+Divide[2b,3ab]
Alternate :
(a^2)/(4ab)+(2b)/(3ab) or a^2/(4ab)+(2b)/(3ab)
Math Input :
Klik di sini(15x^4y^5)/(3xy^2)
Wolfram Language :
Divide[15Power[x,4]Power[y,5],3xPower[y,2]]
Alternate :
(15x^4y^5)/(3xy^2)
Math Input :
Klik di sini(p/q+1/(pq))/(1/q+1)
Wolfram Language :
Divide[Divide[p,q]+Divide[1,(pq)],Divide[1,q]+1]
Alternate :
(p/q+1/(pq))/(1/q+1)
Math Input :
Klik di sini(x^2/y+1/(xy))/(2/x+xy-y)
Wolfram Language :
Divide[Divide[Power[x,2],y]+Divide[1,(xy)],Divide[2,x]+xy-y]
Alternate :
(x^2/y+1/(xy))/(2/x+xy-y)
Math Input :
Klik di sini(3m^2n^3p)/(5mn^2)+(4mn^4p)/(2m^2n)
Wolfram Language :
Divide[3Power[m,2]Power[n,3]p,5mPower[n,2]]+Divide[4mPower[n,4]p,2Power[m,2]n]
Alternate :
(3m^2n^3p)/(5mn^2)+(4mn^4p)/(2m^2n)
Math Input :
Klik di sinisqrt((49x^4y^6)/(16x^2y^2))
Wolfram Language :
Sqrt[Divide[49Power[x,4]Power[y,6],16Power[x,2]Power[y,2]]]
Alternate :
sqrt((49x^4y^6)/(16x^2y^2)) or √((49x^4y^6)/(16x^2y^2))
Math Input :
Klik di sini
Old(x+sqrt(2))/(y-sqrt(3))
Wolfram Language :
Divide[x+Sqrt[2],y-Sqrt[3]]
Alternate :
(x+sqrt(2))/(y-sqrt(3)) or (x+√2)/(y-√3)
Math Input :
Klik di sini3. Persamaan Linear 1 Variabel
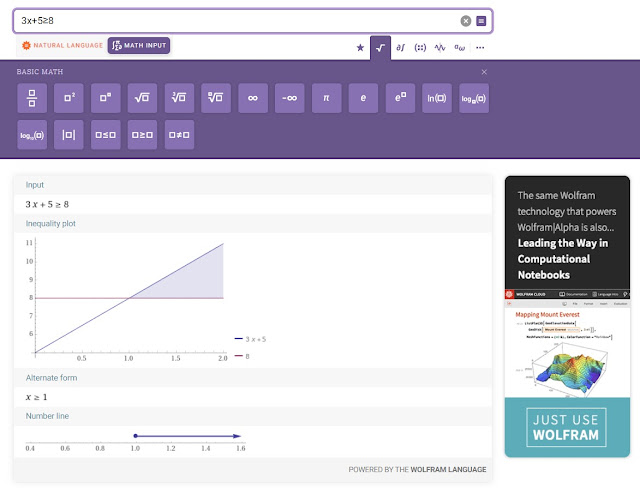
2x+5 = 2
4x-3 = 5
|x+1| = 2
Wolfram Language :
Abs[x+1]=2
Alternate :
abs(x+1)=2 or |x+1|=2
Math Input :
Klik di sinix^2+1=8
Wolfram Language :
Power[x,2]+1=8
Alternate :
x^2+1=8
Math Input :
Klik di sinix^2-2x+3=0
x^3+5x^2-x+2=0
x^4+3x^3-x^2+5x-3=0
Wolfram Language :
Power[x,4]+3Power[x,3]-Power[x,2]+5x-3=0
Alternate :
x^4+3x^3-x^2+5x-3=0
Math Input :
Klik di sinixsqrt(3)-sqrt(2) = sqrt(5)
Wolfram Language :
xSqrt[3]-Sqrt[2] = Sqrt[5]
Alternate :
xsqrt(3)-sqrt(2) = sqrt(5) or x√3-√2 = √5
Math Input :
Klik di sinix/3+5/2=10
5/(x-7)-2/(x+2)=0
Wolfram Language :
Divide[5,x-7]+Divide[2,x+2]=0
Alternate :
5/(x-7)-2/(x+2)=0
Math Input :
Klik di sini(4x+2)/(x-2)=(2x-3)/(x+5)
Wolfram Language :
Divide[4x+2,x-2]=Divide[2x-3,x+5]
Alternate :
(4x+2)/(x-2)=(2x-3)/(x+5)
Math Input :
Klik di sini(7x+6)/(x-4)+(5x-1)/(2x+3)-1/(x^2-7x+12)=1
Wolfram Language :
Divide[7x+6,x-4]+Divide[5x-1,2x+3]-Divide[1,x^2-7x+12]=1
Alternate :
(7x+6)/(x-4)+(5x-1)/(2x+3)-1/(x^2-7x+12)=1
Math Input :
Klik di sini1+x/(2+x/(3+x/4))=0
Wolfram Language :
1+Divide[x,2+Divide[x,3+Divide[x,4]]]=0
Alternate :
1+x/(2+x/(3+x/4))=0
Math Input :
Klik di sinix-1/(2x+1/(3x-1/(4x+1/5x)))=0
Wolfram Language :
x-Divide[1,2x+Divide[1,3x-Divide[1,4x+Divide[1,5x]]]]=0
Alternate :
x-1/(2x+1/(3x-1/(4x+1/5x)))=0
Math Input :
Klik di sini4. Pertidaksamaan Linear 1 Variabel
x+1>5
Wolfram Language and Alternate :
x+1>5
Math Input :
Klik di sini
(x+2)/2≥2
Wolfram Language :
Divide[x+2,2]≥2
Alternate :
(x+2)/2≥2 or (x+2)/2>=2
Math Input :
Klik di sini
2x^2-x≥0
Wolfram Language :
2Power[x,2]-x≥0
Alternate :
2x^2-x≥0 or 2x^2-x>=0
Math Input :
Klik di sini|2x+3|≤7
Wolfram Language :
Abs[2x+3]≤7
Alternate :
abs(2x+3)≤7 or |2x+3|≤7 or |2x+3|<=7
Math Input :
Klik di sinisqrt(x+2)≥x-10
Wolfram Language :
Sqrt[x+2]≥x-10
Alternate :
sqrt(x+2)≥x-10 or √(x+2)≥x-10 or √(x+2)>=x-10 or √(x+2)=>x-10
Math Input :
Klik di sini6/(2x-8)-4/(2x+3)>0
Wolfram Language :
Divide[6,2x-8]-Divide[4,2x+3]>0
Alternate :
6/(2x-8)-4/(2x+3)>0
Math Input :
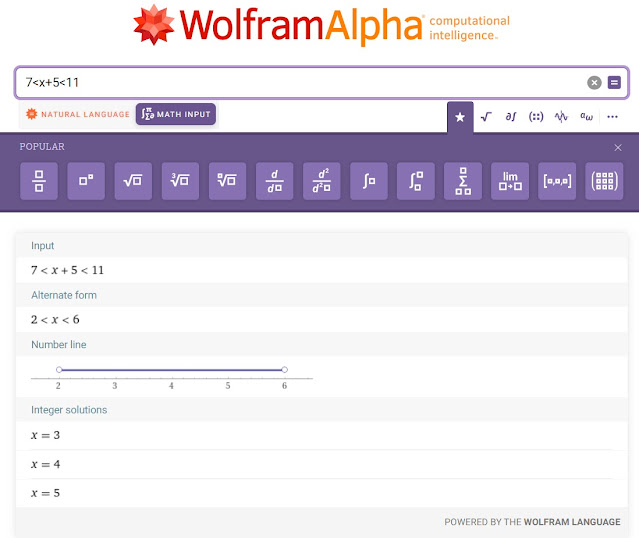
Klik di sini
-4≤x+2≤6
Wolfram Language and Alternate :
-4≤x+2≤6
Math Input :
Klik di sini1<x^2-5≤12
Wolfram Language :
1 < Power[x,2]-5 ≤ 12
Alternate :
1<x^2-5≤12 or 1<x^2-5<=12
Math Input :
Klik di sini5. Persamaan & Pertidaksamaan Lainnya
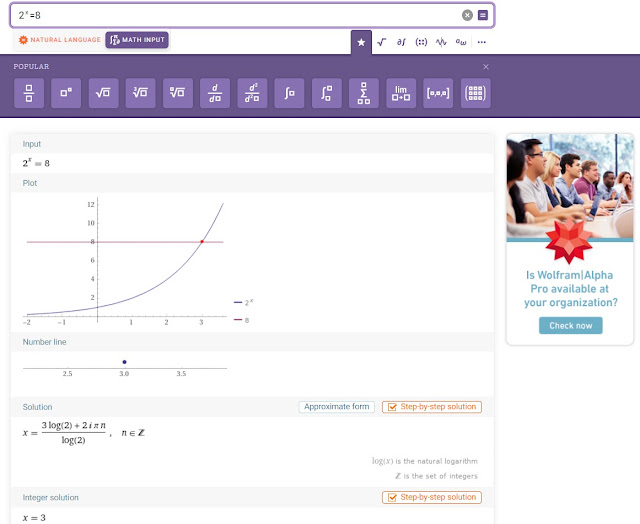
2^x=8
Wolfram Language :
Power[2,x]=8
Alternate :
2^x=8
Math Input :
Klik di sini3^(x+2)=27
4^(x+5)=2^(2x-3)
Wolfram Language :
Power[4,x+5]=Power[2,2x-3]
Alternate :
4^(x+5)=2^(2x-3)
Math Input :
Klik di sini8^(x-2)=sqrt(8)
Wolfram Language :
Power[8,x-2]=Sqrt[8]
Alternate :
8^(x-2)=sqrt(8) or 8^(x-2)=√8
Math Input :
Klik di sini2e^x+5=115
Wolfram Language :
2Power[e,x]+5=115
Alternate :
2e^x+5=115
Math Input :
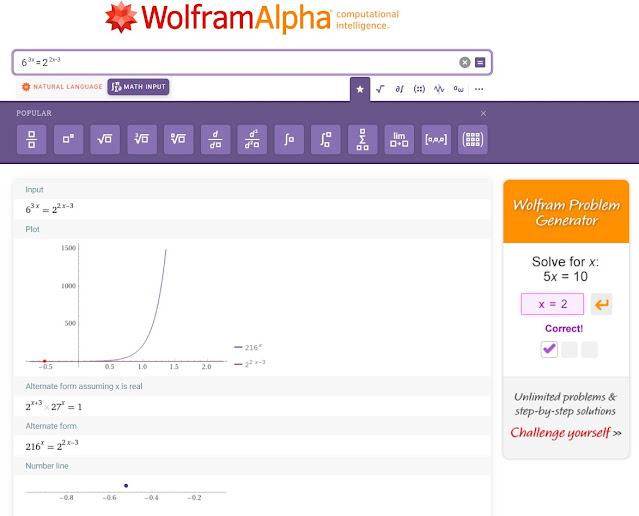
Klik di sini6^(3x)=2^(2x-3)
Wolfram Language :
Power[6,3x]=Power[2,2x-3]
Alternate :
6^(3x)=2^(2x-3)
Math Input :
Klik di sini
Wolfram Language :
Divide[Power[x,4]-1,x-1]=15
Alternate :
(x^4-1)/(x-1)=15
Math Input :
Klik di sini(x^2-2x+1)^(2x+5)=50
Wolfram Language :
Power[x^2-2x+1,2x+5]=50
Alternate :
(x^2-2x+1)^(2x+5)=50
Math Input :
Klik di sinie^x>10
.jpg)
Wolfram Language :
Power[e,x]>10
Alternate :
e^x>10
Math Input :
Klik di sini11^x≥22
.jpg)
Wolfram Language :
Power[11,x]≥22
Alternate :
11^x≥22 or 11^x>=22 or 11^x=>22
Math Input :
Klik di sini3^(2x+7) ≤ 9^(x-4)
%20%E2%89%A4%209%5E(x-4)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[3,2x+7]≤Power[9,x-4]
Alternate :
3^(2x+7)≤9^(x-4) or 3^(2x+7)<=9^(x-4)
Math Input :
Klik di sinix^x≥100
.jpg)
Wolfram Language :
Power[x,x]≥100
Alternate :
x^x≥100 or x^x>=100 or x^x=>100
Math Input :
Klik di sini(x+1)^x≠20
%5Ex%E2%89%A020%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[x+1,x]≠20
Alternate :
(x+1)^x≠20
Math Input :
Klik di sini%5Bgeq%5D20%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[Power[x,3]-1,x-1]>20
Alternate :
(x^3-1)/(x-1)>20
Math Input :
Klik di siniC. Fungsi
Fungsi yang dimaksud di sini adalah Fungsi Trigonometri, Hiperbolik, Logaritma, hingga Fungsi-fungsi Ekstensi lainnya. Dan juga ada Fungsi-fungsi Sederhana seperti Fungsi Abstrak, Floor/Ceiling Function, Sign Function, Hasil Bagi, dan lain-lainnya. Agar lebih mengetahuinya, lihatlah Tabel berikut ini :
Notation | Name | S&O | Graham et al. | |
-- | Ceiling, Least Integer | Ceiling[x] | ||
mod(m, n) | -- | -- | Mod[m, n] | |
Int(x) | Floor, Greatest Integer, Integer Part | Floor[x] | ||
Fractional Value | frac(x) | Fractional Part or {x} | SawtoothWave[x] | |
Fp(x) | No name | |||
Ip(x) | No name | IntegerPart[x] | ||
nint(x) | -- | -- | Round[x] | |
m\n | -- | -- | Quotient[m, n] |
1. Fungsi Abstrak dan yang berkaitan
|-2|
Wolfram Language :
Abs[-2]
Alternate :
abs(-2) or |-2|
Math Input :
Klik di sini
|3+7i|
Wolfram Language :
Abs[3+7i]
Alternate :
abs(3+7i) or |3+7i|
Math Input :
Klik di sini|2-i|
5+|-3|
6-|-2i|
4*|5i|
3/|-7i|
|-3+i|+|-2-3i|
Wolfram Language :
Abs[-3+i]+Abs[-2-3i]
Alternate :
abs(-3+i)+abs(-2-3i) or |-3+i|+|-2-3i|
Math Input :
Klik di sini|5+i|*|1-3i|
Wolfram Language :
Abs[5+i]*Abs[1-3i]
Alternate :
abs(5+i)*abs(1-3i) or |5+i|*|1-3i|
Math Input :
Klik di sini|8-2i|/|7+10i|
Wolfram Language :
Divide[Abs[8-2i],Abs[7+10i]]
Alternate :
abs(8-2i)/abs(7+10i) or |8-2i|/|7+10i|
Math Input :
Klik di sini|x|/θ(x)+δ(x)/x
,%CE%B8(x))+div(%CE%B4(x),x)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[Abs[x],UnitStep[x]]+Divide[DiracDelta[x],x]
Alternate :
abs(x)/unitstep(x)+diracdelta(x)/x or |x|/θ(x)+δ(x)/x
Math Input :
Klik di sini2. Logaritma Sederhana
ln(2)
log(100)
log(2,8)
Wolfram Language :
Log[2,8]
Alternate :
log(2,8)
Math Input :
Klik di siniln(729)/ln(3)
Wolfram Language :
Divide[Log[729],Log[3]]
Alternate :
log(729)/log(3)
Math Input :
Klik di sinilog(5,8)+log(5,3)
Wolfram Language :
Log[5,8]+Log[5,3]
Alternate :
log(5,8)+log(5,3)
Math Input :
Klik di sinilog(5,64)*log(2,5)
Wolfram Language :
Log[5,64]*Log[2,5]
Alternate :
log(5,64)*log(2,5)
Math Input :
Klik di sini1+log(3+log(4,5),2)
Wolfram Language :
1+Log[3+Log[4,5],2]
Alternate :
1+log(3+log(4,5),2)
Math Input :
Klik di sini3. Aljabar Logaritma
log(c,ax+b)
log(a,a)-log(a,c)
Wolfram Language :
Log[a,a]-Log[a,c]
Alternate :
log(a,a)-log(a,c)
Math Input :
Klik di sinilog(a,xy)+log(b,x/y)
Wolfram Language :
Log[a,xy]+Log[b,Divide[x,y]]
Alternate :
log(a,xy)+log(b,x/y)
Math Input :
Klik di sinilog(b,x^p)-log(a,root(x,p))
Wolfram Language :
Log[b,x^p]-Log[a,Surd[x,p]]
Alternate :
log(b,x^p)-log(a,root(x,p))
Math Input :
Klik di sinilog(c,a)*log(b,c)
4. Persamaan & Pertidaksamaan Logaritma
log(5,x) = 2
Wolfram Language :
Log[5,x] = 2
Alternate :
log(5,x) = 2
Math Input :
Klik di sinilog(x,1024) = 5
Wolfram Language :
Log[x,1024] = 5
Alternate :
log(x,1024) = 5
Math Input :
Klik di sini
log(2,x+1) = log(3,27)
Wolfram Language :
Log[2,x+1] = Log[3,27]
Alternate :
log(2,x+1) = log(3,27)
Math Input :
Klik di siniln(x+2)-ln(x+1)=1
Wolfram Language :
Log[x+2]-Log[x+1]=1
Alternate :
log(x+2)-log(x+1)=1
Math Input :
Klik di siniln(x)+ln(x-1)=ln(4x+16)
Wolfram Language :
Log[x]+Log[x-1]=Log[4x+16]
Alternate :
log(x)+log(x-1)=log(4x+16)
Math Input :
Klik di sini4+log(3,9x)=10
ln(10)-ln(6-x)=ln(x)
Wolfram Language :
Log[10]-Log[6-x]=Log[x]
Alternate :
log(10)-log(6-x)=log(x)
Math Input :
Klik di sinilog(2,2x^2-5x)=3+log(2,x-1)
Wolfram Language :
Log[2,2Power[x,2]-5x]=3+Log[2,x-1]
Alternate :
log(2,2x^2-5x)=3+log(2,x-1)
Math Input :
Klik di sinilog(3,x^2-2x+3)=log(2,3x+2)
Wolfram Language :
Log[3,Power[x,2]-2x+3]=Log[2,3x+2]
Alternate :
log(3,x^2-2x+3)=log(2,3x+2)
Math Input :
Klik di sini1+log(2+log(3+log(4,x),x),x)=0
Wolfram Language :
1+Log[2+Log[3+Log[4,x],x],x]=0
Alternate :
1+log(2+log(3+log(4,x),x),x)=0
Math Input :
Klik di sinix-log(2x+log(3x-log(4x+log(5x,2),2),2),2)=1
Wolfram Language :
x-Log[2x+Log[3x-Log[4x+Log[5x,2],2],2],2]=1
Alternate :
x-log(2x+log(3x-log(4x+log(5x,2),2),2),2)=1
Math Input :
Klik di sinilog(6,4x-3)<2
log(x^2-10)>log(x)
Wolfram Language :
Log[10,x^2-10]>Log[10,x]
Alternate :
log(10,x^2-10)>log(10,x)
Math Input :
Klik di sinilog(4,x+3)-log(4,x+2) ≥ 3/2
Wolfram Language :
Log[4,x+3]-Log[4,x+2]≥Divide[3,2]
Alternate :
log(4,x+3)-log(4,x+2)≥3/2 or log(4,x+3)-log(4,x+2)>=3/2
Math Input :
Klik di sinilog(5,x^2-2x+3) ≤ log(4,3x+2)
Wolfram Language :
Log[5,x^2-2x+3]≤Log[4,3x+2]
Alternate :
log(5,x^2-2x+3)≤log(4,3x+2) or log(5,x^2-2x+3)<=log(4,3x+2)
Math Input :
Klik di sini5. Fungsi Trigonometri
sin(60°)
cos(π/4)
1-cot^2(30°)
Wolfram Language :
1-Power[Cot[30°],2]
Alternate :
1-cot^2(30°) or 1-cot^2(30 deg)
Math Input :
Klik di sinisec(π/4+1)
+1)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Sec[Divide[π,4]+1]
Alternate :
sec(π/4+1) or sec(pi/4+1)
Math Input :
Klik di sinicsc((5π)/4)
+1)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Csc[Divide[5π,4]]
Alternate :
csc((5π)/4) or csc((5pi)/4)
Math Input :
Klik di sinisin(2)+cos(3)
+cos(3)%20(Math%20Input%20Wolfram%20Alpha).jpg)
cos(60°)+sin(30°)
+sin(30%C2%B0)%20(Math%20Input%20Wolfram%20Alpha).jpg)
sin(x)+cos(x)
+cos(x)%20(Math%20Input%20Wolfram%20Alpha).jpg)
(tan(30°)+tan(15°))/(1-tan(30°)tan(15°))
+tan(15%C2%B0)),(1-tan(30%C2%B0)tan(15%C2%B0)))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[(Tan[30°]+Tan[15°]),(1-Tan[30°]Tan[15°])]
Alternate :
(tan(30°)+tan(15°))/(1-tan(30°)tan(15°))
Math Input :
Klik di sini2sin(3)cos(3)
cos(3)%20(Math%20Input%20Wolfram%20Alpha).jpg)
2sin(π/3)cos(π/3)
)cos(div(%CF%80,3))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
2Sin[π/3]Cos[π/3]
Alternate :
2sin(π/3)cos(π/3) or 2sin(pi/3)cos(pi/3)
Math Input :
Klik di sinicos^2(45°)+sin^2(45°)
+sin%5E2(45%C2%B0)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[Cos[45°],2]+Power[Sin[45°],2]
Alternate :
cos^2(45°)+sin^2(45°)
Math Input :
Klik di sini(2tan(x))/(1-tan^2(x))
,1-tan%5E2(x))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[(2Tan(x)),(1-Power[Tan[x],2])]
Alternate :
(2tan(x))/(1-tan^2(x))
Math Input :
Klik di sini(2tan(60°))/(1-tan^2(60°))
,1-tan%5E2(60%C2%B0))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[(2Tan(60°)),(1-Power[Tan[60°],2])]
Alternate :
(2tan(60°))/(1-tan^2(60°))
Math Input :
Klik di siniarcsin(2/5)
)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcSin[Divide[2,5]]
Alternate :
arcsin(2/5) or sin^-1(2/5)
Math Input :
Klik di siniarccos(1/6)
)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcCos[Divide[1,6]]
Alternate :
arccos(1/6) or cos^-1(1/6)
Math Input :
Klik di siniarctan(5/3)
)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcTan[Divide[5,3]]
Alternate :
arctan(5/3) or tan^-1(5/3)
Math Input :
Klik di siniarccot(2/3)
)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcCot[Divide[2,3]]
Alternate :
arccot(2/3) or cot^-1(2/3)
Math Input :
Klik di siniarcsec(1/4)
)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcSec[Divide[1,4]]
Alternate :
arcsec(1/4) or sec^-1(1/4)
Math Input :
Klik di siniarccsc(3/7)
)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcCsc[Divide[3,7]]
Alternate :
arccsc(3/7) or csc^-1(3/7)
Math Input :
Klik di sini6. Persamaan Trigonometri
sin(x)+cos(x)=1
+cos(x)=1%20(Math%20Input%20Wolfram%20Alpha).jpg)
2sin^2(x)-cos(x)-1=0
-cos(x)-1=0%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
2Power[Sin[x],2]-Cos[x]-1=0
Alternate :
2sin^2(x)-cos(x)-1=0
Math Input :
Klik di sinitan(x+1)=sqrt(3)+sqrt(3)cot(x)
=sqrt(3)+sqrt(3)cot%E2%81%A1(x)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Tan[x+1]=Sqrt[3]+Sqrt[3]Cot[x]
Alternate :
tan(x+1)=sqrt(3)+sqrt(3)cot(x) or tan(x+1)=√3+√3cot(x)
Math Input :
Klik di sinisin(π/6)=2x/(1-x^2)
)=div(2x,(1-x%5E2))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Sin[Divide[π,6]]=Divide[2x,1-Power[x,2]]
Alternate :
sin(π/6)=2x/(1-x^2)
Math Input :
Klik di sinisec(x)tan(x)=π/3
tan(x)=div(%CF%80,3)%20(Math%20Input%20Wolfram%20Alpha).jpg)
3^sin(x)*cos(x)-3^cos(x)*sin(x)=0
cos%E2%81%A1(x)-3%5Ecos%E2%81%A1(x)sin(x)=0%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[3,Sin(x)]Cos(x)-Power[3,Cos(x)]Sin(x)=0
Alternate :
3^sin(x)cos(x)-3^cos(x)sin(x)=0
Math Input :
Klik di sini2^sin(x)+2^cos(x)=2
+2%5Ecos%E2%81%A1(x)=2%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[2,Sin[x]]+Power[2,Cos[x]]=2
Alternate :
2^sin(x)+2^cos(x)=2
Math Input :
Klik di sini5^sin(x)-4^cos(x)=3
-4%5Ecos%E2%81%A1(x)=3%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[5,Sin[x]]-Power[4,Cos[x]]=3
Alternate :
5^sin(x)-4^cos(x)=3
Math Input :
Klik di sini7. Fungsi Hiperbolik
sinh(1)
%20(Math%20Input%20Wolfram%20Alpha).jpg)
cosh(4)
%20(Math%20Input%20Wolfram%20Alpha).jpg)
sinh(x)+cosh(x)
+cosh(x)%20(Math%20Input%20Wolfram%20Alpha).jpg)
(tanh(8)-tanh(3))/(1-tanh(8)tanh(3))
-tanh%E2%81%A1(3)),(1-tanh%E2%81%A1(8)tanh%E2%81%A1(3)))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[(Tanh(8)-Tanh(3)),(1-Tanh(8)Tanh(3))]
Alternate :
(tanh(8)-tanh(3))/(1-tanh(8)tanh(3))
Math Input :
Klik di sinisinh(5)/sqrt(2(cosh(5)+1))+sqrt((cosh(5)+1)/2)
,sqrt(2(cosh%E2%81%A1(5)+1)))+sqrt(div((cosh%E2%81%A1(5)+1),2))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Divide[Sinh[5],Sqrt[2(Cosh[5]+1)]]+Sqrt[Divide[(Cosh[5]+1),2]]
Alternate :
sinh(5)/sqrt(2(cosh(5)+1))+sqrt((cosh(5)+1)/2) or sinh(5)/√(2(cosh(5)+1))+√((cosh(5)+1)/2)
Math Input :
Klik di sinisech(2)+csch(2)
+csch(2)%20(Math%20Input%20Wolfram%20Alpha).jpg)
coth(4)-tanh(1)
-tanh(1)%20(Math%20Input%20Wolfram%20Alpha).jpg)
arcsinh(2)+arccosh(2)
+arccosh%E2%81%A1(2)%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcSinh[2]+ArcCosh[2]
Alternate :
arcsinh(2)+arccosh(2)
Math Input :
Klik di siniarctanh(1/2)+arccoth(3/2)
)+arccoth%E2%81%A1(div(3,2))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcTanh[Divide[1,2]]+ArcCoth[Divide[3,2]]
Alternate :
arctanh(1/2)+arccoth(3/2)
Math Input :
Klik di siniarcsech(1/4)-arccsch(3/4)
)-arccsch%E2%81%A1(div(3,4))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
ArcSech[Divide[1,4]]-ArcCsch[Divide[3,4]]
Alternate :
arcsech(1/4)-arccsch(3/4)
Math Input :
Klik di sini8. Persamaan Hiperbolik
sinh(x/2)=1
)=1%20(Math%20Input%20Wolfram%20Alpha).jpg)
cosh(x)=2
=2%20(Math%20Input%20Wolfram%20Alpha).jpg)
cosh(x)+tanh(x)=3
+tanh(x)=3%20(Math%20Input%20Wolfram%20Alpha).jpg)
sinh(x)+tanh(x)=4
+tanh(x)=4%20(Math%20Input%20Wolfram%20Alpha).jpg)
sinh^2(x)-cosh(x)-1=0
-cosh%E2%81%A1(x)-1=0%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
Power[Sinh[x],2]-Cosh[x]-1=0
Alternate :
sinh^2(x)-cosh(x)-1=0
Math Input :
Klik di sinicosh(x)coth(x)=100
coth%E2%81%A1(x)=100%20(Math%20Input%20Wolfram%20Alpha).jpg)
){kind=link}
5cosh(x/5)=5/2(e^(x/5)+e^(-x/5))
)=div(5,2)(e%5Ediv(x,5)+e%5E-div(x,5))%20(Math%20Input%20Wolfram%20Alpha).jpg)
Wolfram Language :
5Cosh[Divide[x,5]] = 5/2(Power[e,Divide[x,5]]+Power[e,-Divide[x,5]])
Alternate :
5cosh(x/5)=5/2(e^(x/5)+e^(-x/5))
Math Input :
Klik di siniUntuk melihat Postingan Artikel terdahulu di Blog ini, silakan lihat di sini.
Jadi jika dulu (Sebelum Juli 2021), kita harus mempelajari Bahasa Wolfram (Wolfram Language) terlebih dahulu untuk memasukkan (Input) Rumus-rumus Matematika yang Rumit dan Kompleks. Kini, tak perlu ribet lagi karena sudah ada Math Input di Wolfram|Alpha.
Nantikan untuk Rumus-rumus Matematika dengan Math Input Wolfram|Alpha di Part 2 nanti seperti Vektor dan Matriks, Prakalkulus, Kalkulus, hingga Transformasi dalam Matematika.
Terima Kasih 😄😘👌👍 :)
Wassalamu‘alaikum wr. wb.
Post a Comment