Pengertian dan Contoh dari Stack & Queue (Beserta Program dalam C++) (+ Video Materi)

Assalamu‘alaikum wr. wb.

Halo gais, Kembali lagi bersama Inzaghi's Blog! Jika sebelumnya di Algoritma kita sudah membahas tentang Linked List. Kali ini kita akan membahas tentang Stack dan Queue. Kali ini saya akan membahasnya lebih lanjut pada Artikel ini.

STACK

Sumber Materi : Pintarkom.com

Stack atau tumpukan adalah kumpulan elemen yang hanya dapat ditambah dan atau dihapus dari satu ujung (gerbang) yang sama. Hal ini menunjukkan bahwa seolah-olah suatu elemen diletakkan di atas elemen yang lain. Yang memberi gambaran bahwa Stack mempunyai sifat LIFO (Last In First Out) yang berarti bahwa elemen yang terakhir masuk akan pertama keluar.

Representasi Stack dapat dilakukan menggunakan Array atau Linked List. Kedua representasi mempunyai keunggulan dan kelemahan. Pada bab ini Stack direpresentasikan dengan kedua cara tersebut. Representasi Stack dengan Array dapat dilakukan dengan asumsi bahwa elemen maksimal suatu Stack tidak boleh melebihi maksimum banyak elemen atau ukuran Array. Untuk menjaga hal ini terjadi maka harus ada penunjuk atau suatu nama yang mencatat posisi puncak elemen Stack. Dengan Array, Stack juga dapat disajikan dengan Single Stack dan Double Stack.

Secara sederhana, sebuah Stack dapat dilihat pada Gambar di bawah. Misalkan kita mempunyai 6 buah kotak yang ditumpukkan. Koak A diletakkan pertama sekali kemudian diikuti secara berturut-turut dengan kotak B, kotak C, kotak D, kotak E, dan terakhir kotak F. Maka untuk mengambil tiap kotak dari tumpukan harus dilakukan secara berturut-turut mulai dari kotak F, kotak E, kotak D, kotak C, kotak B, kemudian kotak A. Karena jika kita membutuhkan kotak C misalnya dan langsung mengambil kotak C tanpa terlebih dahulu mengambil kotak di atasnya maka tumpukan akan tumbang.

A. Deklarasi Stack

Suatu stack dapat dideklarasikan dengan dua cara berikut ini, tetapi di sini yang akan digunakan adalah dengan bentuk deklarasi yang kedua.

Bentuk Deklarasi Pertama :

#define MaxS n
TypeData Isi(MaxS);
TypeData Top;

Bentuk Deklarasi Kedua :

#define MaxS n
struct Stack
{
     TypeData Isi(MaxS);
     TypeData Top;
};

B. Operasi pada Stack

Ada 2 (Dua) Operasi Dasar yang dapat dilakukan terhadap sebuah Stack, yaitu operasi Insert atau penyisipan Elemen yang sering disebut istilah PUSH dan operasi Delete atau penghapusan Elemen yang sering disebut istilah POP.

1. Inisialisasi Stack

Sebelum Stack dapat dioperasikan terlebih dahulu diinisialisasikan dengan memberi harga S.Top = 0.

void INITS (Stack &S)
{
     S.Top = 0;
}

2. Operasi PUSH

Operasi PUSH adalah operasi memasukkan elemen ke dalam suatu Stack. Jika Stack direpresentasikan dengan menggunakan Array, maka elemen array yang dimasukkan tidak boleh melebihi ukuran Stack. Maka dengan demikian harus ada nama sebagai penunjuk posisi elemen Puncak (Top) dari Stack dan penunjuk isi maksimum dari Stack (Max). Operasi PUSH dapat dilakukan jika Stack belum mencapai Max.

Misalkan diketahui suatu Stack S dengan maksimum 5 elemen. Andaikan elemen-elemen A, B, C, D, dan E dimasukkan (PUSH) secara berturut-turut maka elemen A akan menempati posisi pertama (1), elemen B pada posisi ke-2, elemen C pada posisi ke-3, elemen D pada posisi ke-4, dan elemen E pada posisi ke-5. Operasi penyisipan elemen dapat dilihat pada Gambar di bawah ini.

Perhatikan bahwa petunjuk Max tidak pernah bergerak. Yang bergerak adalah Top. Petunjuk Top akan bertambah satu jika ada elemen masuk (PUSH) ke dalam Stack hingga Top = Max. Gambar a merupakan suatu Stack kosong, dengan Top=0 dan Max=5. Gambar b menunjukkan penyisipan elemen A sehingga Top=1 dan Max=5. Gambar c menunjukkan penyisipan elemen B sehingga Top=2 dan Max=5. Gambar d menunjukkan penyisipan elemen C sehingga Top=3 dan Max=5. Gambar e menunjukkan penyisipan elemen D sehingga Top=4 dan Max=5. Gambar f menunjukkan penyisipan elemen E sehingga Top=5 dan Max=5 yang menyatakan Stack Penuh.

Fungsi PUSH untuk memasukkan elemen ke Stack adalah seperti berikut.

void PUSH(Stack &S, char Data) {
    if(S.Top < MaxS) {
        S.Top++;
        S.Isi[S.Top] = Data;
    }
    else
        cout<<"Stack Penuh ......";
}

3. Operasi POP

Operasi mengambil atau menghapus elemen paling puncak dari Stack. Setiak kali operasi POP dilakukan maka petunjuk Top akan berkurang satu. Operasi POP dapat dilakukan jika Stack tidak kosong.

Misalkan kita punya Stack seperti pada Gambar diatas (f) akan dilakukan penghapusan elemen demi elemen. Ilustrasi penghapusan elemen dapat dilihat pada Gambar di bawah ini.

Gambar a merupakan suatu Stack Penuh, dengan Top=Max. Gambar b menunjukkan penghapusan elemen E sehingga Top=4 dan Max=5. Gambar c menunjukkan penghapusan elemen D sehingga Top=3 dan Max=5. Gambar d menunjukkan penghapusan elemen C sehingga Top=2 dan Max=5. Gambar e menunjukkan penghapusan elemen B sehingga Top=1 dan Max=5. Gambar f menunjukkan penghapusan elemen A sehingga Top=0 dan Max=5 menyatakan Stack Kosong.

Fungsi POP untuk menghapus elemen dari Stack adalah seperti berikut.

void POP(Stack &S, char &Hsl) {
    if(S.Top != 0) {
        Hsl = S.Isi[Top];
        S.Top--;
    }
    else
        cout<<"Stack Kosong ......";
}

4. Mencetak Stack

Isi suatu Stack dapat dicetak dengan menggunakan fungsi berikut.

void CETAK(Stack S){
    int i;
    cout<<endl<<"Isi Stack : ";
    if (S.Top != 0){
        for(i=0;i<=S.Top;i++)
        cout<<S.Isi[i];
    }
    else
    
        cout<<"Stack Kosong ......";
}

5. Operasi FULL

Operasi FULL adalah operasi yang akan digunakan untuk mengecek apakah Stack penuh atau tidak. Suatu Stack dikatakan penuh jika S.Top bernilai MaxS (S.Top=MaxS). Jika S.Top=MaxS maka fungsi akan mengembalikan nilai true, jika tidak maka fungsi akan mengembalikan nilai false. Operasi ini dibuat dalam fungsi FULL.

int FULL(void){
    if(S.Top == MaxS) return(true);
    else return(false);
}

6. Operasi Empty

Operasi Empty adalah operasi yang akan digunakan untuk mengecek apakah Stack kosong atau tidak. Suatu Stack dikatakan kosong jika S.Top bernilai nol (S.Top=0). Maka jika S.Top=0 maka fungsi akan mengembalikan nilai true, jika tidak maka fungsi akan mengembalikan nilai false. Operasi ini dibuat dalam fungsi Empty.

int Empty(void){
    If(S.Top == 0) return(true);
    else return(false);
}

7. Operasi Clear

Operasi Clear adalah operasi yang akan digunakan untuk mengosongkan Stack. Suatu Stack dikatakan kosong jika Top=0. Operasi ini dibuat dalam fungsi Clear sebagai berikut.

int Clear(void){
    S.Top = 0;
}

C. Karakteristik Suatu Stack

Dari operasi yang dilakukan di atas dapat kita peroleh bahwa karakteristik dari suatu Stack adalah :

• Elemen Stack yaitu item-item data yang terdapat dalam Stack.
• Top menunjukkan posisi puncak pada Stack.
• Max menunjukkan banyaknya maksimum item dari Stack.
• Stack Kosong tidak mungkin dilakukan POP karena akan menyebabkan Error
• Stack Penuh tidak mungkin dilakukan PUSH karena akan menyebabkan Error

D. Penerapan Stack

Stack dapat diaplikasikan untuk :

• Simulasi Stack dalam dunia nyata
• Pemanggilan fungsi/procedure
• Rekursif
• Penanganan Interupsi
• Evaluasi Ekspresi
• Konversi Notasi Infiks ke Notasi Postfiks
• Konversi Sistem Bilangan, misalnya dari Basis 10 (Desimal) ke Basis 2 (Biner)

E. Ekspresi Aritmatika

Ekspresi Aritmatika terdiri dari operator, operand, dan pembatas. Ekspresi Aritmatika dapat dituliskan dalam 3 bentuk, yaitu notasi infiks, notasi prefiks, dan notasi postfiks. Notasi yang biasa digunakan oleh manusia adalah notasi infiks karena lebih mudah dimengerti. Namun dalam mengevaluasi suatu notasi infiks harus memperhatikan prioritas dari operator yang ada. Misalnya, jika kita mempunyai ekspresi A+B*C maka urutan prosesnya adalah:

• Kalikan nilai B terhadap nilai C.
• Jumlahkan nilai A terhadap hasil perkalian di atas.

Dari urutan di atas kita lihat bahwa karena prioritas perkalian (*) lebih tinggi dibanding dengan penjumlahan, maka operator perkalian dikerjakan terlebih dahulu baru penjumlahan. Berbeda dengan ekspresi ((A+B)*C). Ekspresi ini akan dioperasikan dengan urutan :

• Jumlahkan nilai A terhadap nilai B.
• Kalikan hasil perjumlahan di atas terhadap nilai B.

Dari urutan di atas dapat kita lihat bahwa walaupun prioritas operator perkalian lebih tinggi dibandingkan dengan prioritas perjumlahan, tetapi karena adanya padangan tanda buka tutup kurung maka akan mengubah urutan prosesnya. Pasangan buka tutup kurung lebih tinggi dibandingkan dengan perkalian.

Berbeda dengan komputer, pada saat kompilasi program semua notasi ekspresi aritmatika dalam notasi infiks akan diubah ke dalam notasi postfiks dengan menggunakan operasi Stack.

• Notasi Infiks       : A + B
• Notasi Prefiks     : + A B
• Notasi Postfiks   : A B +

1. Konversi Ekspresi

Ekspresi Aritmatika dalam notasi tertentu dapat dikonversikan ke notasi yang lain dengan tanpa menggunakan Stack. Sedangkan dengan menggunakan Stack hanya dapat dilakukan konversi notasi infiks ke notasi postfiks.

a. Konversi Notasi Tanpa Menggunakan Stack

    1.) Konversi Notasi Infiks ke Notasi Prefiks dan Postfiks

Yang perlu diperhatikan dalam konversi notasi infiks ke notas yang lain hanya prioritas masing-masing operator yang ada dalam notasi infiks. Operator dengan prioritas tertinggi pertama dilakukan. Jika terdapat dua atau lebih operator dengan prioritas yang sama maka akan dikerjakan mulai dari yang kiri.

Misalnya : A + B * C / D – E

Operator * → Ambil Operand sebelum dan sesudahnya : B dan C

Maka ekspresi di atas menjadi A + 1 / D – E

Operator / → Ambil Operand sebelum dan sesudahnya : 1 dan D

Maka ekspresi di atas menjadi A + 2 – E

Operator + → Ambil Operand sebelum dan sesudahnya : A dan 2

Maka ekspresi di atas menjadi 3 – E

Operator – → Ambil operand sebelum dan sesudahnya : 3 dan E

Prefiks                  : -3E

Postfiks                : 3E-

Lakukan substitusi untuk memperoleh notasi yang selengkapnya untuk notasi Prefiks dan Postfiks.

Prefiks                  : -3E = -+A2E = -+A/1DE = -+A/*BCDE

Postfiks                : 3E- = A2E- = A1D/E- = ABC*D/E-       

    2.) Konversi Notasi Prefiks ke Notasi Infiks dan Postfiks

Konversi notasi prefiks ke notasi infiks atau postfiks dilakukan dengan cara mengambil operator mulai dari kanan ke kiri kemudian diikuti dengan mengambil dua operand sebelumnya. Tapi untuk notasi infiks harus dituliskan dalam pasangan buka tutup kurung.

Misalnya : -+A/*BCDE

Operator * → Ambil 2 Operand sebelumnya : B dan C

Maka ekspresi di atas menjadi : -+A/1DE

Operator / → Ambil 2 Operand sebelumnya : 1 dan D

Maka ekspresi di atas menjadi : -+A2E

Operator + → Ambil 2 Operand sebelumnya : A dan 2

Maka ekspresi di atas menjadi : -3E.

Operator – → Ambil 2 Operand sebelumnya : 3 dan E

Infiks                    : (3-E)

Postfiks                : 3E-   

Lakukan substitusi untuk memperoleh notasi yang selengkapnya untuk notasi infiks dan postfiks.

Infiks                    : (3 – E) = ((A+2) – E) = ((A+(1/D)) – E = ((A+((B*C)/D)) – E)

Postfiks                : 3E- = A2+E- = A1D/+E- = ABC*D/+E-                                   

    3.) Konversi Notasi Postfiks ke Notasi Infiks dan Postfiks

Konversi notasi prefiks ke notasi infiks atau postfiks dilakukan dengan cara mengambil operator mulai dari kiri ke kanan kemudian diikuti dengan mengambil dua operand sebelumnya. Tapi untuk notasi infiks harus dituliskan dalam pasangan buka tutup kurung.

Misalnya : ABC*D/+E-

Operator * → Ambil 2 Operand sebelumnya : B dan C

Maka ekspresi di atas menjadi : A1D/+E-

Operator / → Ambil 2 Operand sebelumnya : 1 dan D

Maka ekspresi di atas menjadi : A2+E-

Operator + → Ambil 2 Operand sebelumnya : A dan 2

Maka ekspresi di atas menjadi : 3E-

Operator – → Ambil 2 Operand sebelumnya : 3 dan E

Infiks                     : (3 – E)

Prefiks                  : -3E     

Lakukan substitusi untuk memperoleh notasi yang selengkapnya untuk notasi infiks dan prefiks.

Infiks                    : (3 – E) = ((A+2) – E) = ((A+(1/D)) – E) = ((A+((B*C)/D)) – E)

Prefiks                  : -3E = -+A2E = -+A/1DE = -+A/*BCDE                                   

b. Konversi Notasi Infiks Menggunakan Stack

Ekspresi aritmatika yang dapat dikonversi dengan menggunakan Stack adalah hanya dari notasi infiks ke notasi postfiks. Notasi infiks dapat dibedakan dengan dua bentuk, yaitu infiks tanpa pasangan buka tutup kurung dan dengan pasangan buka tutup kurung lengkap yang disebut istilah Well Form Formula (WFF). Konversi notasi ini juga berbeda.

    1.) Notasi Infiks Tak Bertanda Kurung

Untuk mengkonversi notasi infiks tak bertanda kurung ke notasi postfiks dapat dilakukan dengan :

• String infiks merupakang suatu ekspresi infiks tak bertanda kurung valid.
• Satu Stack diinisiasikan kosong.
• String postfiks diinisiasikan dengan ⁿⁿ (null string) untuk menampung hasil konversi.
• Perhatikan tingkat kekutan/prioritas simbol, pada Tabel di bawah.

Langkah-langkah konversi notasi infiks ke Notasi Postfiks.

Scan simbol dari kiri ke kanan ekspresi infiks dan setiap kali scan simbol infiks bandingkan simbol yang di-scan dengan simbol yang ada pada Stack (posisi TOP) saat itu :

• Jika tingkat kekuatan simbol di Stack Lebih Besar atau Sama Dengan tingkat kekuatan simbo yang di scan maka simbo yang di Stack Disambung (Concate) dengan string postfiks.
• Jika tingkat kekuatan simbol di Stack Lebih Kecil dengan tingkat kekuatan simbol yang di scan atau Stack Kosong maka simbol yang di scan Dimasukkan (PUSH) ke dalam Stack.
• Jika infiks telah Kosong maka POP semua isi Stack satu persatu dan Concate dengan string postfiks.

Contoh : 5*2+4^3/8-7 → 52*43^8/+7-

    2.) Notasi Infiks Bertanda Kurung Lengkap

Konversi notasi infiks bertanda kurung lengkap dapat dilakukan dengan :

• String infiks merupakan suatu ekspresi infiks bertanda kurung valid.
• Tanda kurung buka pada string infiks masuk ke Stack tetapi tidak masuk ke dalam string postfiks.
• Tanda kurung buka pada stack nilai prioritasnya berubah menjadi 0.
• Tanda kurung tutup di-scan maka elemen puncak Stack hingga kurung buka di concate terhadap string postfiks.
• Tanda kurung tutup tidak pernah masuk ke dalam Stack.

Perhatikan tingkat kekuatan atau prioritas simbol pada Tabel di bawah.

Langkah-langkah konversi notasi infiks bertanda kurung lengkap ke Notasi Postfiks :

Scan simbol dari kiri ke kanan ekspresi infiks dan setiap kali scan simbol infiks bandingkan simbol yang di scan (fungsi f) dengan simbol yang ada pada posisi puncak (Top) Stack (fungsi g) saat itu :

• Jika prioritas simbol di Stack (fungsi g) lebih besar dengan prioritas simbol yang di scan (fungsi f) maka simbol yang di Stack disambung (Concate) dengan string Postfiks.
• Jika tingkat kekuatan simbol di Stack lebih kecil atau sama dengan tingkat kekuatan simbol yang di scan atau Stack kosong maka simbol yang di scan dimasukkan (PUSH) ke dalam Stack.

Contoh : ((5*((2+4)^3))/(8-7)) → 524+3^*87-/

2. Evaluaasi Ekspresi

a. Evaluasi Notasi Postfiks

Untuk mengevaluasi suatu ekspresi dalam notasi postfiks dilakukan dengan langkah-langkah berikut :

• Buat Stack kosong.
• Ambil elemen satu persatu dari kiri.
• Jika elemen itu adalah operand maka masukkan ke Stack, dan jika operator maka keluarkan dua nilai teratas dari Stack (operand2 dan operand1) lalu hitung dengan operator yang bersangkutan, hasilnya masukkan ke dalam Stack. Perlu diperhatikan bahwa jika tidak ada 2 operand dalam Stack, maka ada kesalahan pada notasi tersebut.
• Ulangi langkah ke-2 dan ke-3 sampai elemen dalam notasi postfiks habis. Jika telah habis, maka elemen yang tinggal adalah elemen hasil.

Contoh : Evaluasi ekspresi notasi postfiks dengan menggunakan Stack : 7 8 2 * 4 / – 3 2 ^ + –

Operasi Evaluasi Ekspresi 7 8 2 * 4 / – 3 2 ^ +

b. Evaluasi Notasi Prefiks

Untuk mengevaluasi suatu ekspresi dalam notasi prefiks dilakukan dengan langkah-langkah berikut :

• Buat Stack kosong.
• Ambil elemen satu persatu dari kanan.
• Jika elemen itu adalah operand maka masukkan ke Stack, dan jika operator maka keluarkan dua nilai teratas dari Stack (operand1 dan operand2) lalu hitung dengan operator yang bersangkutan, hasilnya masukkan ke dalam Stack. Perlu diperhatikan bahwa jika tidak ada 2 operand dalam Stack, maka ada kesalahan pada notasi tersebut.
• Ulangi langkah ke-2 dan ke-3 sampai elemen dalam notasi prefiks habis. Jika telah habis, maka elemen yang tinggal adalah elemen hasil.

Contoh : Evaluasi ekspresi notasi Prefiks dengan menggunakan Stack : + – 7 / * 8 2 4 ^ 3 2

Operasi Evaluasi Ekspresi + – 7 / * 8 2 4 ^ 3 2

Berikut ini adalah program lengkap dari suatu Stack dengan menggunakan Array.

#include <iostream.h>
#include <conio.h>
#define MaxS 10
struct Stack {
    char Isi[MaxS];
    unsigned int Top;
};
void INITS (Stack &S);
void PUSH(Stack &S, char Data);
void CETAK(Stack S);
void POP(Stack &S, char &Hsl);
main() {
    char huruf;
    Stack S;
    
    INITS(S);
    cout<<"Masukkan Karakter  :";
    cin>>huruf;
    PUSH(S,huruf);
    cout<<"Masukkan Karakter  :";
    cin>>huruf;
    PUSH(S,huruf);
    cout<<"Masukkan Karakter  :";
    cin>>huruf;
    PUSH(S,huruf);
    CETAK(S);
    POP(S,huruf);
    cout<<endl<<"Yang Dihapus ...."<<huruf;
    CETAK(S);
    cout<<endl<<"Masukkan Karakter :";
    cin>>huruf;
    PUSH(S,huruf);
    cout<<"Masukkan Karakter  :";
    cin>>huruf;
    PUSH(S,huruf);
    cout<<"Masukkan Karakter  :";
    cin>>huruf;
    PUSH(S,huruf);
    CETAK(S);
    POP(S,huruf);
    cout<<endl<<"Yang Dihapus ...."<<huruf;
    CETAK(S);
    getch();
}
void INITS (Stack &S) {
    S.Top = 0;
}
void PUSH(Stack &S, char Data) {
    if (S.Top < MaxS) {
        S.Top++;
        S.Isi(S.Top) = Data;
    }
    else
        cout<<"Stack Penuh ......";
}
void CETAK(Stack S) {
    int i;
    cout<<endl<<"Isi Stack  : ";
    if (S.Top != ) {
        for(i=1;i<=S.Top;i++) {
          cout<<S.Isi[i];
        }
    }
    else {
        cout<<"Stack Kosong ....";
    }
}
void POP(Stack &S, char &Hsl) {
    if (S.Top != 0) {
        Hsl = S.Isi[S.Top];
        S.Top--;
    }
    else {
        cout<<"Stack Kosong ....";
    }
}

F. Stack dengan Linked List

Representasi Stack dengan menggunakan Linked List, penyisipan elemen dilakukan dengan sisip belakang dan pengambilan/penghapusan elemen dilakukan dengan hapus belakang pada Single List atau Double List.

Berikut ini merupakan program lengkap Stack dengan menggunakan Singly Linked List.

#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
#define true 1
#define false 0
typedef struct node *simpul;
struct node {
    char Isi;
    simpul next;
};
//======================
//==Prototype Function==
//======================
void Sisip_Belakang(simpul &L, char elemen);
void Hapus_Belakang(simpul &L);
void Cetak(simpul L);
//=================
//==Function Main==
//=================
main() {
    char huruf
    simpul L = NULL  //Pastikan bahwa L kosong
    cout<<"==OPERASI SINGLE LINKED LIST PADA STACK==\n\n";
    //==================
    //==Sisip Belakang==
    //==================
    cout<<endl<<endl<<"Penyisipan Stack "<<endl<<endl;
    cout<<"Masukkan Elemen  :"; cin>>huruf;
    Sisip_Belakang(L, huruf);
    cout<<"Masukkan Elemen  :"; cin>>huruf;
    Sisip_Belakang(L,huruf);
    cout<<"Masukkan Elemen  :"; cin>>huruf;
    Sisip_Belakang(L, huruf);
    cout<<"Masukkan Elemen  :"; cin>>huruf;
    Sisip_Belakang(L,huruf);
    cout<<"Masukkan Elemen  :"; cin>>huruf;
    Sisip_Belakang(L,huruf);
    cout<<"Masukkan Elemen  :"; cin>>huruf;
    Sisip_Belakang(L,huruf);
    Cetak(L);
    //=========================
    //==Hapus Simpul Belakang==
    //=========================
    cout<<endl<<endl<<"Hapus Elemen "<<endl;
    Hapus_Belakang(L);
    Cetak(L);
    cout<<endl<<endl<<"Hapus Elemen "<<endl;
    Hapus_Belakang(L);
    Cetak(L);
    cout<<endl<<endl<<"Hapus Elemen "<<endl;
    Hapus_Belakang(L);
    Cetak(L);
    cout<<endl<<endl<<"Hapus Elemen "<<endl;
    Hapus_Belakang(L);
    Cetak(L);
    getch();
}
//*************************************
//**FUNCTION SISIP SIMPUL DI BELAKANG**
//*************************************
void Sisip_Belakang(simpul &L, char elemen) {
    simpul bantu, baru;
    baru = (simpul) malloc(sizeof(simpul));
    baru->Isi = elemen;
    baru->Next = NULL;
    if(L == NULL)
        L=baru;
    else {
        bantu=L;
        while(bantu->next != NULL) {
            bantu=bantu->next;
        }
        bantu->next=baru;
    }
}
//**********************************
//**FUNCTION HAPUS SIMPUL BELAKANG**
//**********************************
void Hapus_Belakang(simpul &L) {
    simpul bantu, hapus;
    if(L==NULL) {
        cout<<"Linked List Kosong .................";
    }
    else {
        bantu = L;
        while(bantu->next->next != NULL)
          bantu=bantu->next;
        hapus = bantu->next;
        bantu->next = NULL;
        free(hapus);
    }
}
//*************************************
//**FUNCTION MENCETAK ISI LINKED LIST**
//*************************************
void Cetak(simpul L) {
    simpul bantu;
    if(L==NULL) {
        cout<<"Linked List Kosong .................";
    }
    else {
        bantu=L;
        cout<<endl<<"Isi Linked List  : ";
        while (bantu->next != NULL) {
            cout<<bantu->Isi<<"->";
            bantu=bantu->next;
        }
        cout<<bantu->Isi;
    }
}

G. Double Stack

Double Stack merupakan pengembangan dari Single Stack dengan maksud menghemat memori. Stack 1 bergerak dari kiri (posisi 0) ke kanan sedangkan Stack 2 bergerak dari kanan (posisi MaxS) ke kiri. Stack 1 dikatakan kosong jika Top1=0, dan Stack2 dikatakan kosong jika Top2=MaxS+1. Double Stack dikatakan penuh jika Top2 = Top1 + 1. Setiap penyisipan elemen ke Stack 1 maka Top1 naik satu dan penyisipan elemen ke Stack maka Top2 kurang satu. Penyisipan elemen dapat dilakukan selama Top2 tidak sama dengan Top1 + 1.

Berikut program lengkap double stack.

#include<iostream.h>
#include<conio.h>
#define Max 20
struct Stack {
    char Isi[Max+1];
    unsigned int top1;
    unsigned int top2;
};
void init (Stack &S);
void Push(Stack &S, int nostack, char Data);
void baca(Stack S, int nostack);
void Pop(Stack &S, char &Hsl, int nostack);
int Full(Stack S);
int empty(int nostack);
void clear(Stack &S, int nostack);
main() {
    char huruf;
    Stack S;
    int k, nomor;
    init(S);
    cout<<"Mengisi Stack Pertama..."<<endl<<endl;
    for(k=1;k<=5;k++) {
      cout<<"Masukkan Karakter :";
      cin>>huruf;
      Push(S,1,huruf);  //mengisi huruf ke Stack1
    }
    baca(S,1);  //mencetak isi Stack Pertama
    cout<<"\n\nMengisi Stack Kedua..."<<endl<<endl;
    for(k=1;k<=5;k++) {
      cout<<"Masukkan Karakter :";
      cin>>huruf;
      Push(S,2,huruf);  //mengisi huruf ke Stack2
    }
    baca(S,2);  //mencetak isi Stack
    cout<<"\n\nmenghapus elemen Stack Pertama..."<<endl;
    Pop(S,huruf,1);  //Menghapus elemen puncak Stack;
    cout<<"elemen Yang dihapus : "<<huruf<<endl;
    baca(S,1);  //mencetak isi Stack
    cout<<"\n\nmenghapus elemen Stack Kedua..."<<endl;
    Pop(S,huruf,2);  //Menghapus elemen puncak Stack 2
    cout<<"elemen Yang dihapus : "<<huruf<<endl;
    baca(S,2);  //mencetak isi Stack
    cout<<"\n\nMengisi Stack Kedua...\n\n";
    for(k=1;k<=3;k++) {
      cout<<"Masukkan Karakter :";
      cin>>huruf;
      Push(S,2,huruf);  //mengisi huruf ke Stack2
    }
    baca(S,2);  //mencetak isi Stack
    cout<<"\n\nmenghapus elemen Stack Kedua..."<<endl;
    Pop(S,huruf,2);  //Menghapus elemen puncak Stack 2
    cout<<"elemen Yang dihapus : "<<huruf<<endl;
    baca(S,2);  //mencetak isi Stack 2
    cout<<"\n\nmenghapus elemen Stack Kedua..."<<endl;
    Pop(S,huruf,2);  //Menghapus elemen puncak Stack 2
    cout<<"elemen Yang dihapus : "<<huruf<<endl;
    baca(S,2);  //mencetak isi Stack 2
    cout<<"Masukkan Karakter  : "; cin>>huruf;
    cout<<"Masukkan Nomor Stack  : "; cin>>nomor;
    Push(S,nomor,huruf);
    baca(S,nomor);
    for(k=1;k<=3;k++) {
      cout<<"Masukkan Karakter  : "; cin>>huruf;
      cout<<"Masukkan Nomor Stack  : "; cin>>nomor;
      Push(S,nomor,huruf);
    }
    baca(S,1);
    baca(S,2);
    
    getch();
}
/*  ===================
  ==Fungsi Inisiasi==
  =================== */
void init(Stack &S) {
  S.top1 = 0;
  S.top2 = Max+1;
}
/*  =====================================
  ==Fungsi Memasukkan Elemen ke Stack==
  ===================================== */
void Push(Stack &S, int nostack, char Data) {
    if(Full(S) != true) {
      switch(nostack) {
        case 1 : S.top1++;
            S.Isi[S.top1] = Data;
        break;
        case 2 : S.top2--;
            S.Isi[S.top2] = Data;
        break;
        default: cout<<"Invalid PUSH..."<<endl;
        break;
      }
    }
    else {
        cout<<"Stack Over....."<<endl;
    }
}
/*  ======================================
  ==Fungsi Menghapus Elemen dari Stack==
  ====================================== */
void Pop(Stack &S, char &Hsl, int nostack) {
  switch (nostack) {
    case 1 : Hsl = S.Isi[S.top1];
          S.top1--;
    break;
    case 2 : Hsl = S.Isi[S.top2];
          S.top2++;
    break;
    default: cout<<"invalid POP...."<<endl;
    break;
  }
}
/*  =============================
  ==Fungsi Mengosongkan Stack==
  ============================= */
void clear(Stack &S, int nostack) {
    switch(nostack) {
        case 1 : S.top1 = 0;
        break;
        case 2 : S.top2 = Max+1;
        break;
        default: cout<<"Nomor Stack Invalid...\n";
        break;
    }
}
/*  ===============
  ==Fungsi FULL==
  =============== */
int Full(Stack S) {
  if(S.top1 + 1 >= S.top2) return (true);
  else return(false);
}
/*  ========================================
  ==Fungsi Membaca/Mencetak Elemen Stack==
  ======================================== */
void baca(Stack S, int nostack) {
    int i;
    switch(nostack) {
        case 1 : cout<<"Isi Stack Pertama : ";
            for(i=1;i<=S.top1;i++)
            cout<<S.Isi[i];
        break;
        case 2 : cout<<endl<<"Isi Stack Kedua : ";
            for(i=Max;i>=S.top2;i--)
            cout<<S.Isi[i];
    }
    cout<<endl;
}

QUEUE

Sumber Materi : Pintarkom.com

Queue atau Antrean merupakan kumpulan elemen dengan penyisipan dan penghapusan elemen yang dilakukan dari sisi/gerbang yang berbeda. Penyisipan dilakukan dari gerbang belakang dan penghapusan dilakukan dari gerbang depan. Hal ini menunjukkan bahwa untuk Queue mempunyai dua gerbang yaitu gerbang depan dan gerbang belakang. Dengan demikian dapat dilihat bahwa Queue mempunyai sifat FIFO (First In First Out), yaitu elemen yang pertama masuk akan keluar pertama juga. Untuk lebih jelas perhatikan ilustrasi pada Gambar di bawah. yang menunjukkan Queue dengan 5 Elemen.

Dari Queue di atas kita lihat bahwa 5 elemen (A,B,C,D,E) dimasukkan secara berturut-turut dari belakang. Maka Elemen A yang merupakan elemen pertama masuk sehingga menempati posisi paling depan, Elemen E yang merupakan elemen terakhir masuk sehingga elemen E menempati posisi paling belakang.

A. Linier Queue dengan Array

Jika menggunakan array maka ada penunjuk depan dan belakang yang digunakan untuk menunjukkan elemen posisi depan dan elemen posisi belakang sehingga dapat diketahui Queue kosong atau tidak. Queue dapat ditambah selama belakang tidak sama dengan maksimum isi array.

1. Deklarasi Queue

#define MaxQ N
#define true 1
#define false 0
struct Queue
     {
           TypeData Isi[MaxQ+1];
           TypeData Depan;
           TypeData Belakang;
     };

2. Operasi pada Linear Queue

Sama halnya dengan Stack, operasi yang dapat dilakukan pada suatu Queue pada dasarnya adalah penyisipan elemen dan penghapusan elemen. Di samping itu juga dapat dilakukan operasi untuk mengecek apakah Queue kosong atau penuh.

a. Operasi Inisialisasi

Operasi ini digunakan untuk menginisialisasikan suatu Queue, yaitu dengan memberi nilai depan=1 dan nilai belakang=0. Dengan kata lain digunakan untuk membuat suatu Queue yang baru.

void INITS (Queue &Q)
{
     Q.Depan = 1;
     Q.Belakang = 0;
}

b. Operasi Queue Kosong

Operasi ini digunakan untuk mengecek apakah suatu Queue dalam keadaan kosong atau tidak. Karena pada saat penghapusan elemen Queue, harus dijamin bahwa Queue tidak boleh kosong. Dikatakan suatu Queue kosong adalah jika penunjuk belakang=0. Operasi ini dibuat dalam suatu fungsi, sehingga fungsi akan mengembalikan nilai true jika Queue kosong, tetapi fungsi akan mengembalikan nilai false jika Queue tidak kosong.

int Empty (void)
{
     if(Q.Belakang == 0) return (trues);
     else return(false)
}

c. Operasi Queue Penuh

Operasi ini digunakan untuk mengecek apakah suatu Queue dalam keadaan penuh atau tidak. Karena pada saat penyisipan elemen Queue, harus dijamin bahwa Queue tidak dalam keadaan penuh. Suatu Queue dikatakan penuh jika penunjuk belakang=MaxQ. Operasi ini dibuat dalam suatu fungsi, sehingga akan mengembalikan nilai true jika Queue penuh, tetapi fungsi akan mengembalikan nilai false jika Queue tidak penuh.

int FULL (void)
{
     if(Q.Belakang == MaxQ) return(trues);
     else return(false)
}

d. Operasi Mengosongkan Queue

Operasi ini digunakan untuk membuat Queue dalam keadaan kosong dari Queue dalam keadaan tidak kosong. Operasi ini berbeda dengan operasi inisialisasi Queue, karena dalam operasi inisialisasi dilakukan untuk Queue yang belum pernah ada. Sedangkan pada operasi ini Queue sebelumnya sudah ada dan karena sesuatu hal misalnya Queue akan dikosongkan.

void KOSONG(Queue &Q)
{
     Q.Belakang=0;
}

e. Operasi Penyisipan Elemen Queue

Operasi ini digunakan untuk menyisipkan elemen ke dalam Queue. Elemen dapat disisipkan ke dalam Queue selama Queue tidak dalam keadaan penuh. Setiap penyisipan elemen dilakukan maka penunjuk belakang akan bertambah satu. Penunjuk tidak boleh bergerak (naik ataupun turun). Untuk jelasnya perhatikan Gambar di bawah. sebagai ilustrasi penyisipan elemen Queue.

Dari gambar di atas kita lihat bahwa gambar (a) menunjukkan bahwa Queue dalam keadaan kosong. Gambar (b) menunjukkan bahwa elemen A disisipkan ke Queue sehingga penunjuk Blk (Belakang) naik satu. Demikian seterusnya hingga elemen Q disisipkan dan penunjuk Blk sama dengan MaxQ.

Berikut fungsi yang digunakan untuk menyisipkan elemen ke dalam suatu Queue.

void EnQueue(Queue &Q, typeData Data)
{
     if (Q.Belakang < MaxQ)
     {
           Q.Belakang++;
           Q.Isi(Q.Belakang) = Data;
     }
     else
           cout<<"Queue Penuh .......";
}

f. Operasi Penghapusan Elemen Queue

Operasi ini digunakan untuk menghapus elemen dari Queue. Elemen dalam suatu Queue dapat dihapus selama Queue tidak dalam keadaan kosong. Setiap penghapusan elemen dilakukan maka semua elemen berikutnya harus bergeser satu posisi ke depan kemudian penunjuk belakang akan berkurang satu. Penunjuk depan tidak boleh bergerak (naik ataupun turun). Untuk jelasnya perhatikan Gambar di bawah. sebagai ilustrasi penghapusan elemen Queue.

g. Operasi Pencetakan Isi Queue

Operasi ini digunakan untuk mencetak elemen-elemen isi dari suatu Queue. Berikut fungsi untuk mencetak elemen Queue.

void CETAK(Queue Q)
{
     int;
     cout<<endl<<"Isi Queue : ";
     if(Q.Belakang >= Q.Depan)
     {
           for(i=1;i<=Q.Belakang;i++)
           {
                cout<<Q.Isi[i];
           }
     }
     else
           cout<<"Queue Kosong....";
}

B. Circular Queue dengan Array

Kelemahan dari Delete Queue adalah setiap melakukan penghapusan harus diikuti dengan pergeseran dari setiap elemen yang ada dalam Queue satu posisi ke depan. Untuk mengatasi kelemahan ini dapat dilakukan dengan Queue Melingkar (Circular Queue).

Circular Queue adalah suatu Queue yang dibuat seakan-akan merupakan sebuah lingkaran. Misalkan kita mempunyai suatu Queue dengan maksimal 8 elemen yang dibuat secara melingkar seperti pada Gambar di bawah ini.

Circular Queue dengan 8 Elemen

1. Deklarasi Circular Queue

Deklarasi Linier Queue sama dengan deklarasi Circular Queue yaitu Depan=1 dan Belakang=0.

#define MaxQ N
struct Queue
{
     TypeData Isi[MaxQ+1];
     TypeData Depan;
     TypeData Belakang;
};

2. Operasi pada Circular Queue

a. Operasi Inisialisasi

Operasi ini digunakan untuk menginisialisasikan suatu Queue, yaitu dengan memberi nilai Depan=1 dan nilai Belakang=0. Dengan kata lain operasi ini digunakan untuk membuat suatu Queue yang baru.

void INITS(Queue &Q)
{
     Q.Depan = 1;
     Q.Belakang =0;
}

b. Operasi Penyisipan Elemen Queue

Operasi ini digunakan untuk menyisipkan elemen ke dalam Queue. Setiap kali elemen dimasukkan ke Queue maka penunjuk belakang naik 1 (Belakang+1) jika belakang lebih dari maksimum elemen array. Tetapi jika belakang sama dengan maksimum elemen array maka belakang diset menjadi 1 (Belakang=1). Elemen dapat dimasukkan ke dalam Queue selama Queue belum penuh. Suatu Queue dikatakan penuh jika Depan=1 dan Belakang=Maksimum atau Depan-Belakang=1. Gambar di bawah merupakan ilustrasi penyisipan elemen ke dalam Queue dengan maksimum 8 elemen.

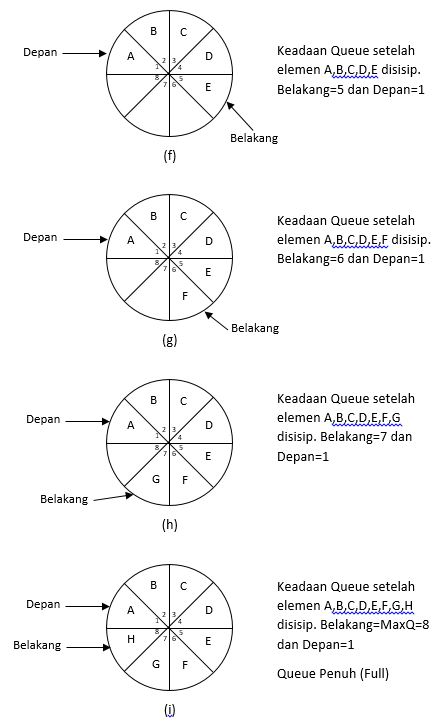Operasi Penyisipan Elemen Pada Circular Queue

Dari gambar di atas dapat kita lihat bahwa penyisipan elemen, penunjuk belakang selalu bertambah satu jika belakang masih lebih kecil dari maksimum. Queue penuh jika Depan=1 dan Belakang=Maksimum. Suatu Queue juga dikatakan penuh jika Depan – Belakang = 1. Perhatikan Gambar di bawah.

Queue Penuh

Berikut ini fungsi yang digunakan untuk menyisipkan elemen ke dalam Queue.

void ENQUEUE (Queue &Q, typeData Data)
{
     if((Q->Belakang==MaxQ) && (Q->Depan==1)) || (Q->Depan-Q->Belakang == 1)
           cout<<"Queue Penuh ....";
     else
     {
           if(Q->Belakang == MaxQ) && (Q->Depan > i)
                Q->Belakang = 1;
           else
                Q->Belakang++;
           Q->Isi(Q->Belakang)=Data;
     }
}

c. Operasi Penghapusan Elemen Queue

Operasi ini digunakan untuk mengambil atau menghapus elemen dari suatu Queue. Operasi penghapusan elemen pada Circular yang dihapus adalah selalu yang ada di depan sehingga penunjuk depan akan naik satu (Depan+1) jika depan lebih kecil dari maksimum elemen array. Tetapi depan diset menjadi satu (Depan=1) jika depan sama dengan maksimum elemen array.

Misalkan kita memiliki Queue yang pernah seperti pada Gambar di bawah ini akan dilakukan penghapusan elemen.

Perhatikan gambar di atas. Setiap kali penghapusan elemen maka depan akan naik satu atau diset menjadi 1. Operasi penghapusan dapat dilakukan selama  Queue belum kosong.

Dari gambar di atas dapat dilihat bahwa suatu Queue dikatakan :

• Kosong (Empty) adalah jika Depan = 1 dan Belakang = 0 (Depan – Belakang = 1).
• Penuh (Full) adalah jika :
• Belakang = MaxQ dan Depan=1
• Depan – Belakang = 1
• Jika Depan = 3 dan Belakang = 6 maka isi Queue adalah {C, D, E, F}.
• Jika Depan = 6 dan Belakang = 3 maka isi Queue adalah {F, G, H, A, B, C}.
  

Berikut fungsi untuk menghapus elemen dari suatu Circular Queue.

void DEQUEUE (Queue &Q, TypeData Hsl)
{
     if (Q->Depan == 1) && (Q->Belakang==0)
           cout<<"Queue Kosong...";
     else
     {
           Hsl = Q->Isi(Q->Depan);
           if(Q->Depan == MaxQ)
                Q->Depan = 1;
           else
                Q->Depan++;
     }
}

C. Circular Queue Diperbarui

Kelemahan Circular Queue adalah syarat untuk mengecek suatu Queue Kosong dan Penuh sama, yaitu: Depan – Belakang = 1. Hal ini merupakan sesuatu yang kurang baik, sebaiknya syarat untuk kosong harus berbeda dengan syarat untuk penuh.

Maka untuk mengatasi kelemahan dari Circular Queue di atas dapat dilakukan dengan cara “Elemen yang ditunjuk oleh depan tidak digunakan”. Misalnya kita gunakan gambar 9.4 dengan tidak menggunakan Circular Queue yang diperbarui, maka jika :

• Depan = 3 dan Belakang = 6, isi Queue {D, E, F}
• Depan = 6 dan Belakang = 3, isi Queue {G, H, A, B, C}
• Depan = 4 dan Belakang = 5, isi Queue {E}
• Depan = 5 dan Belakang = 4, isi Queue Full
• Depan = 5 dan Belakang = 5, Queue Kosong

a. Operasi Inisialisasi

Berbeda dengan inisialisasi Circular Queue di atas, karena elemen yang ditunjuk oleh depan tidak digunakan, maka penunjuk belakang harus dibuat bernilai 1 (Depan=1 dan Belakang=1).

void Init(Queue &Q)
{
     Q->Depan := 1;
     Q->Belakang := 1;
}

b. Operasi Penyisipan Elemen Queue

Operasi penyisipan ke dalam Queue, hampir sama dengan penyisipan elemen pada Circular Queue, bedanya adalah kalau pada Circular Queue elemen yang disisipkan ditempatkan pada posisi yang ditunjuk oleh belakang. Sedangkan pada Circular Queue yang diperbarui elemen yang disisipkan ditempatkan pada posisi Belakang+1. Perhatikan ilustrasi pada Gambar di bawah ini.

Operasi Penyisipan Elemen pada Circular Queue Diperbarui

Perhatikan Gambar berikut ini merupakan Queue Penuh.

Dari gambar di atas dapat dilihat bahwa suatu Queue dikatakan :

• Kosong jika Depan = Belakang
• Penuh jika Depan – Belakang = 1 atau Depan=1 dan Belakang=Maksimum

Berikut fungsi untuk menyisipkan elemen pada Circular Queue yang diperbarui.

void ENQUEUE(Queue &Q, TypeDataElemen Data)
{
     if(!(Full))
           if(Q->Depan-Q->Belakang!=1) && ((Q.Depan==1) && (Q->Belakang == MaxQ))
           {
                if(Q->Belakang==MaxQ) && (Q->Depan>1)
                      Q->Belakang=1;
                else
                      Q->Belakang++;
                Q->Isi(Q->Belakang) = Data;
           }
                cout<<"Queue Penuh....";
}

Berikut fungsi Full yang digunakan untuk mengecek suatu Queue penuh atau tidak. Fungsi akan mengembalikan nilai true jika Queue penuh atau mengembalikan false jika Queue tidak penuh.

int Full(Queue Q)
{
     if(Q->Depan-Q->Belakang==1) || ((Q->Depan==1) && (Q->Belakang == MaxQ))
           Full = true;
     else
           Full = false;
}

c. Operasi Penghapusan Elemen Queue

Operasi penghapusan elemen ke dalam Queue hampir sama dengan penghapusan elemen pada Circular Queue. Bedanya adalah kalau pada Circular Queue elemen yang dihapus berada pada posisi yang ditunjuk oleh depan. Sedangkan pada Circular Queue yang diperbarui elemen yang dihapus adalah elemen yang berada pada posisi Depan+1 jika depan lebih kecil dari maksimum elemen array. Tetapi elemen yang dihapus adalah elemen yang berada pada posisi 1 jika depan sama dengan maksimum elemen array. Perhatikan ilustrasi pada gambar di bawah ini.

Operasi Penghapusan Elemen pada Circular Queue Diperbarui

Berikut fungsi untuk menghapus elemen dari Queue pada Circular diperbarui.

void DEQUEUE(Queue &Q, TypeDataElemen Hsl)
{
     if(Q->Depan - Q->Belakang != 0)
     {
           if(Q->Depan == MaxQ)
           {
                Hsl = Q->Isi[l];
                Q->Depan = 1;
           }
           else
           {
                Hsl = Q->Isi[Q->Depan+1];
                Q->Depan++;
           }
     }
     else
           cout<<"Queue Kosong....";
}

D. Queue dengan Linked List

Queue dapat juga direpresentasi dengan Linked List (Single List atau Double List). Penyisipan elemen dilakukan dengan sisip belakang dan penghapusan elemen dilakukan dengan hapus depan.

Berikut ini program untuk operasi Queue dengan menggunakan Singly Linked List.

#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
typedef struct node *simpul;
struct node {
    char Isi;
    simpul next;
};
//======================
//==Prototype Function==
//======================
void Sisip_Belakang(simpul &L, char elemen);
void Hapus_Depan(simpul &L);
void Cetak(simpul L);
//==================
//==Function Matin==
//==================
main() {
    char huruf;
    simpul L = NULL;  //Patikan bahwa L kosong
    int i;
    cout<<"==OPERASI PADA SINGLE LINKED LIST=="<<endl<<endl;
    //=================
    //==Sisi Belakang==
    //=================
    cout<<"\nPenyisipan Simpul \n\n";
    for(i=1;i<=3;i++) {
        cout<<"Masukkan Huruf  :";
        cin>>huruf;
        Sisip_Belaakng(L, huruf);
    }
    Cetak(L);
    //======================
    //==Hapus Simpul Depan==
    //======================
    cout<<"\nSetelah Hapus Simpul "<<endl;
    Hapus_Depan(L);
    Cetak(L);
    cout<<"\nSetelah Hapus Simpul "<<endl;
    Hapus_Depan(L);
    Cetak(L);
    cout<<"\nSetelah Hapus Simpul "<<endl;
    Hapus_Depan(L);
    Cetak(L);
    cout<<"\nPenyisipan Simpul \n\n";
    for(i=1;i<=3;i++) {
        cout<<"Masukkan Huruf : ";
        cin>>huruf;
        Sisip_Belakang(L, huruf);
    }
    Cetak(L);
    cout<<"\nSetelah Hapus Simpul "<<endl;
    Hapus_Depan(L);
    Cetak(L);
    cout<<"\nSetelah Hapus Simpul "<<endl;
    Hapus_Depan(L); {
        Hapus = L;
        L = L->next;
        Hapus->next = NULL;
        free(Hapus);
    }
    
}  //====================eof====================

VIDEO MATERI

Untuk memahami lebih lanjut terkait dengan Stack and Queue, lihatlah Video-video YouTube di bawah ini.

Dan untuk membaca Artikel sebelumnya tentang Linked List, silakan lihat di sini. 

Itulah Materi tentang Stack and Queue yang telah saya sampaikan. Mohon maaf apabila ada kesalahan sedikitpun baik itu Penulisan Kata ataupun kesalahan dalam Program.

Terima Kasih 😄😘👌👍 :)

Wassalamu‘alaikum wr. wb.