Assalamu'alaikum Wr. Wb.
Hello semuanya ! Kali ini saya akan menjelaskan tentang Pi Day. Yang bertepatan pada Tanggal 14 Maret 2019 (7 Rajab 1440 H).
Pi (π) adalah sebuah Konstanta dalam Matematika yang merupakan perbandingan Keliling Lingkaran dengan Diameter-nya. Nilai π dalam 20 Digit Desimal adalah 3,14159265358979323846.
Banyak rumus dalam Matematika, Sains, dan Teknik yang menggunakan π, yang menjadikannya salah satu dari konstanta matematika yang penting. Pi (π) adalah Bilangan Irasional, yang berarti nilai π tidak dapat dinyatakan dalam Pembagian Bilangan Bulat (biasanya Pecahan 22/7 digunakan sebagai nilai pendekatan π, namun sebenarnya tiada satupun pecahan yang dapat mewakili nilai yang sama persis dengan π.) Oleh karena itu pula, Representasi Desimal π tidak akan pernah berakhir dan tidak akan pernah memiliki pola angka tertentu yang permanen. Digit-digit desimal π tampaknya terdistribusikan secara acak, walaupun sampai sekarang hal ini masih belum dibuktikan. Pi (π) adalah Bilangan Transedental, yakni bilangan yang bukan akar dari polinom-polinom bukan nol manapun yang memiliki koefisien rasional. Transendensi π memiliki implikasi pada ketidakmungkinan teka-teki matematika kuno "mengkuadratkan lingkaran dengan hanya menggunakan Jangka dan Penggaris" untuk dapat dipecahkan.
Banyak rumus dalam Matematika, Sains, dan Teknik yang menggunakan π, yang menjadikannya salah satu dari konstanta matematika yang penting. Pi (π) adalah Bilangan Irasional, yang berarti nilai π tidak dapat dinyatakan dalam Pembagian Bilangan Bulat (biasanya Pecahan 22/7 digunakan sebagai nilai pendekatan π, namun sebenarnya tiada satupun pecahan yang dapat mewakili nilai yang sama persis dengan π.) Oleh karena itu pula, Representasi Desimal π tidak akan pernah berakhir dan tidak akan pernah memiliki pola angka tertentu yang permanen. Digit-digit desimal π tampaknya terdistribusikan secara acak, walaupun sampai sekarang hal ini masih belum dibuktikan. Pi (π) adalah Bilangan Transedental, yakni bilangan yang bukan akar dari polinom-polinom bukan nol manapun yang memiliki koefisien rasional. Transendensi π memiliki implikasi pada ketidakmungkinan teka-teki matematika kuno "mengkuadratkan lingkaran dengan hanya menggunakan Jangka dan Penggaris" untuk dapat dipecahkan.
(Ada di Wikipedia)
CIRI - CIRI DAN SIFAT DASAR
1. Definisi
Pi (π) umumnya didefinisikan sebagai Rasio Keliling Lingkaran C dengan diameternya d:
Rasio C/d bernilai konstan tak tergantung pada ukuran lingkaran. Contohnya, jika suatu lingkaran memiliki diameter dua kali lipat daripada lingkaran lainnya, ia juga akan memiliki keliling yang dua kali lipat lebih besar, sehingganya nilai rasio C/d akan tetap sama. Definisi π seperti ini secara implisit menggunakan Geometri Euklides. Walaupun gagasan akan lingkaran juga dapat diperluas ke dalam geometri non-Euklides, namun lingkaran yang baru ini tidak akan lagi memenuhi rumus π = C/d. Terdapat pula definisi π lainnya yang tidak menyebut-nyebut lingkaran sama sekali, yakni: π adalah bilangan yang bernilai dua kali lipat dari bilangan positif terkecil x yang mana cos(x) sama dengan 0.
2. Ciri-ciri
Pi (π) adalah Bilangan Irasional, yang berarti bahwa ia tidak dapat ditulis sebagai rasio dua bilangan bulat. Karena π Irasional, maka ia memiliki digit bilangan desimal yang tak terhingga banyaknya. Terdapat beberapa bukti bahwa π irasional. Umumnya pembuktian ini memerlukan kalkulus dan bergantung pada teknik Reductio ad Absurdum. Sejauh mana bilangan π dapat didekati menggunakan Bilangan Rasional tidaklah diketahui.
Pi (π) adalah Bilangan Transendental, yang berarti bahwa ia bukanlah penyelesaian dari Polinom non-konstan berkoefisien Rasional manapun seperti Transendensi π mempunyai dua konsekuensi penting. Pertama, π tidak dapat diekspresikan menggunakan kombinasi bilangan rasional dan akar kuadrat ataupun Akar Pangkat ke-n manapun seperti atau Kedua, oleh karena tiada bilangan transendental apapun yang dapat dikonstruksikan menggunakan jangka dan penggaris, tidaklah dimungkinkan untuk "Mempersegikan Lingkaran". Dengan kata lain, tidaklah mungkin untuk mengkonstruksi persegi yang luasnya sama dengan luas lingkaran tertentu hanya dengan menggunakan jangka dan penggaris. Pemersegian lingkaran merupakan salah satu teka-teki geometri yang penting pada zaman Era Klasik. Matematikawan amatiran pada zaman modern kadang-kadang masih berusaha mempersegikan lingkaran dan mengklaim berhasil menyelesaikannya, walaupun telah diketahui hal ini tidak mungkin dilakukan.
Digit-digit π tidak memiliki pola apapun dan telah melewati uji Keacakan Statistis meliputi uji normalitas; sebuah bilangan dengan panjang tak terhingga dikatakan normal apabila keseluruhan barisan digitnya muncul sama banyaknya. Hipotesis bahwa π adalah normal belum berhasil dibuktikan maupun dibantah. Sejak ditemukannya komputer, sejumlah besar digit π telah berhasil dikomputasi untuk dianalisis secara statistik. Yasumasa Kanada telah menganalisis secara detail digit-digit desimal π dan menemukannya konsisten dengan normalitas. Tiada bukti sepuluh digit 0 sampai dengan 9 yang ditemukan memiliki pola-pola apapun. Walaupun digit-digit π telah melewati uji keacakan statistik, π mengandung beberapa barisan digit yang tampaknya tidak acak, misalnya Titik Feynman, yang merupakan barisan enam angka 9 secara beruruan yang dimulai dari desimal ke-762 π.
3. Nilai Pendekatan / Taksiran
Perhitungan π direvolusi oleh berkembangnya teknik deret tak hingga pada abad ke-16 dan 17. Deret tak hingga merupakan penjumlahan deretan suku-suku yang tak terhingga banyaknya. Hal ini memungkinkan matematikawan menghitung nilai π dengan presisi yang melebihi metode Archimedes. Walaupun metode deret tak hingga utamanya digunakan oleh matematikawan Eropa untuk menghitung nilai π, pendekatan ini pertama kali ditemukan di India antara tahun 1400 dan 1500.
Beberapa Pendekatan dan Basis Bilangan Pi (π) meliputi :
- Bilangan Bulat : 3
- Pecahan : Pendekatan pecahan meliputi : (diurutkan berdasarkan kenaikan akurasi) 227, 333106, 355113, 5216316604, 10399333102, dan 24585092278256779. (Disarikan dari
 A063674 and
A063674 and  A063673.)
A063673.)
 |
| Bilangan Pi (π) jika ditulis dengan Sistem Bilangan Berbasis 60 (Seksagesimal / Sexagesimal) (15 digit pertama) |
Biner / Binary (Basis 2) : 11,001001000011111...[2]
Terneri / Ternary (Basis 3) : 10,010211012222010...[3]
Kuaterneri / Quaternary (Basis 4) : 3,021003331222202...[4]
Kuineri / Quinary (Basis 5) : 3,032322143033432...[5]
Seneri / Senary (Basis 6) : 3,050330051415124...[6]
Septeneri / Septenary (Basis 7) : 3,066365143203613...[7]
Oktal / Octal (Basis 8) : 3,110375524210264...[8]
Noneri / Nonary (Basis 9) : 3,124188124074427...[9]
Desimal / Decimal (Basis 10) : 3,141592653589793...[10]
Undesimal / Undecimal (Basis 11) : 3,16150702865a485...[11]
Duodesimal / Duodecimal (Basis 12) : 3,184809493b91866...[12] atau 3,184809493Ɛ91866...[12]
Tridesimal / Tridecimal (Basis 13) : 3,1ac1049052a2c77...[13]
Tetradesimal / Tetradecimal (Basis 14) : 3,1da75cda8137542...[14]
Pentadesimal / Pentadecimal (Basis 15) : 3,21cd1dc46c2b7e5...[15]
Heksadesimal / Hexadecimal (Basis 16) : 3,243f6a8885a308d...[16]
Vigesimal (Basis 20) : 3,2gceg9gbhj9d21h...[20]
Heksatrigesimal / Hexatrigesimal (Basis 36) : 3,53i5ab8p5fsa5jh...[36] atau 3;5,3,18,5,10,11,8,25,5,15,28,10,5,19,17,...[36]
Seksagesimal / Sexagesimal (Basis 60) : 3;8,29,44,0,47,25,53,7,24,57,36,17,43,4,29,...[60] atau 3,8tι0μpς7oχαhθ4t...[60] [Lihat diatas]
RUMUS - RUMUS YANG DIPAKAI
Berikut, inilah penggunaan Pi (π) dalam beberapa Rumus :
1. Rumus Keliling 단 Luas Lingkaran dan Volume 단 Luas Permukaan 3 Dimensi yang berhubungan dengan Lingkaran
Pi (π) muncul dalam rumus untuk area dan volume bentuk geometris berdasarkan lingkaran, seperti Elips, Bola, Kerucut, dan Torus. Gambar di atas tersebut adalah beberapa rumus yang lebih umum yang melibatkan π.
Integral pasti yang menggambarkan keliling, luas, atau volume bentuk yang dihasilkan oleh lingkaran biasanya memiliki nilai yang melibatkan π. Misalnya, integral yang menentukan setengah luas lingkaran dengan jari yang diberikan oleh :
Dalam integral tersebut, fungsi mewakili kurva setengah lingkaran, dan integralnya menghitung luas antara setengah lingkaran dengan sumbu x.
2. Rumus Trigonometri
 |
| Tabel Sudut Istimewa (Kuadran 1 - 4) |
Fungsi trigonometri bergantung pada sudut, dan matematikawan umumnya menggunakan radian sebagai satuan pengukuran. Pi (π) memainkan peran penting dalam sudut yang diukur dalam radian, yang didefinisikan sehingga lingkaran lengkap merentang sudut 2π radian. Ukuran sudut 180 ° sama dengan π radian, dan 1 ° = π / 180 radian.
 |
| Tabel Fungsi Trigonometri |
 |
| Fungsi Sinus dan Cosinus diulangi dengan Periode 2π. (Sumber : Wikipedia) |
Fungsi-fungsi trigonometri pada umumnya memiliki periode yang merupakan kelipatan dari π, sebagai contohnya sinus dan kosinus memiliki periode 2π, sehingga untuk sudut θ apapun dan bilangan bulat k apapun, dan
3. Bilangan Imajiner dan Analisis Bilangan Kompleks (Imaginary and Complex Numbers Analysics)
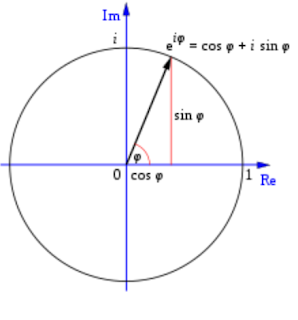
Bilangan kompleks apapun, sebut saja z, dapat dinyatakan menggunakan pasangan bilangan nyata. Dalam sistem koordinat polar, satu bilangan (Jari-jari atau r) digunakan untuk menyatakan jarak z dari pusat bidang kompleks sedangkan (Sudut atau φ) menyatakan a putaran berlawanan arah jarum jam dari garis nyata positif sebagai berikut :
dengan i adalah Satuan Imajiner dari i2 = −1. Setingnya penggunaan π dalam Analisis Kompleks dapat dihubungkan dengan perilaku Fungsi Eksponential variabel kompleks, yang dijelaskan oleh Rumus Euler :
Dengan Tetapan e (e = 2,71828182845904...) adalah basis Logaritma Natural. Formula ini menghasilkan hubungan antara daya Imajiner e dan titik-titik pada Satuan Lingkaran yang berpusat pada pusat bidang kompleks. Pengaturan φ = π dalam formula Euler menghasilkan Identitas Euler, disambut gembira oleh para matematikawan karena mengandung lima tetapan matematika paling penting :
Sebanyak n Bilangan Kompleks z yang berbeda dalam persamaan zn = 1, disebut "Akar Persatuan (Root of Unity) ke n". Mereka dinyatakan dalam persamaan:
Rumus Integral Cauchy mengelola Fungsi Integral Kompleks (Complex Integral Function) dan menghasilkan hubungan penting antara integrasi dan diferensiasi, termasuk kenyataan bahwa nilai fungsi kompleks dalam suatu batas tertutup seluruhnya ditentukan oleh nilai pada batasan :
Keberadaan π dalam Fraktal Himpunan Mandelbrot ditemukan oleh warga negara Amerika David Boll pada tahun 1991. Dia mempelajari perilaku humpunan Mandelbrot dekat "Leher" pada (-0,75, 0). Jika dianggap titik dengan koordinat (-0,75, ε), dengan ε cenderung nol, jumlah iterasi sampai perbedaan untuk jalur dikalikan dengan ε konvergen menuju π. Titik (0,25, ε) di titik puncak "lembah" besar di sisi kanan himpunan Mandelbrot berperilaku sama: jumlah iterasi sampai divergensi dikalikan dengan akar kuadrat ε cenderung mendekati π.
Fungsi Gamma memperluas konsep Faktorial (Biasanya didefinisikan hanya untuk Bilangan Bulat Non-Negatif) ke semua bilangan kompleks, kecuali bilangan bulat nyata negatif. Ketika fungsi gama dievaluasi untuk bilangan setengah bulat, hasilnya berisi π; sebagai contoh :
- dan
- .
Fungsi gama dapat digunakan untuk membuat pendekatan sederhana seperti n! untuk n besar:
Yang dikenal sebagai Aproksimasi Stirling (Stirling Aproximation).
4. Teori bilangan dan Fungsi Zeta Riemann
Fungsi Zeta Riemann ζ(s) digunakan dalam banyak bidang matematika. Ketika dievaluasi pada s = 2 fungsi ini dapat ditulis sebagai:
Menemukan penyelesaian sederhana untuk deret tak hingga ini merupakan masalah populer dalam matematika yang disebut Masalah Basel (Basel's Problem). Leonhard Euler memecahkannya pada tahun 1735 ketika ia menunjukkan bahwa itu sama dengan π2/6. Hasil Euler mengarah pada Teori Bilangan (Number's Teory) yaitu probabilitas dua angka acak yang bersifat Prima Relatif (tidak memiliki faktor bersama) adalah sama dengan 6/π2. Probabilitas ini berdasarkan pengamatan bahwa probabilitas bilangan sembarang dapat dibagi dengan suatu bilangan prima p adalah 1/p (sebagai contoh, setiap bilangan bulat ke-7 dapat dibagi dengan 7.) Sehingga probabilitas dua bilangan yang keduanya dapat dibagi dengan bilangan prima ini adalah 1/p2, dan probabilitas bahwa sekurang-kurangnya satu di antaranya tidak dapat dibagi adalah 1-1/p2. Untuk bilangan prima yang berbeda, kasus dapat dibagi ini bersifat independen; sehingga probabilitas bahwa dua bilangan adalah prima relatif diberikan oleh hasil pembagian seluruh bilangan prima:
Probabilitas ini dapat digunakan bersamaan dengan Generator Bilangan Acak untuk memperkirakan π menggunakan pendekatan Monte Carlo.
5. Probabilitas dan Statistik
Bidang Probabilitas dan Statistik seringkali menggunakan Distribusi Normal sebagai model sederhana untuk fenomena kompleks, sebagai contoh, ilmuwan umumnya berasumsi bahwa kesalahan pengamatan dalam kebanyakan percobaan mengikuti sebuah distribusi normal. Fungsi Gauss (yang merupakan Fungsi Kepekatan Probabilitas distribusi normal) dengan rata-rata μ dan Simpangan Baku σ, pada dasarnya adalah π :
Agar ini dapat menjadi kepekatan probabilitas, wilayah di bawah grafik f harus sama dengan satu. Hal ini diperoleh dari perubahan variabel dalam Integral Gauss :
- ,
sehingga luas daerah yang berada di bawah kurva lonceng sederhana sama dengan akar kuadrat π.
6. Metode Monte Carlo
Metode Monte Carlo, yang mengevaluasi hasil dari banyak percobaan acak, dapat digunakan untuk membuat aproksimasi π. Jarum Buffon adalah salah satu tekniknya: Jika sebuah jarum dengan panjang ℓ dijatuhkan n kali di atas permukaan yang di atasnya digambar garis paralel yang dipisahkan sebesar t satuan, dan jika dari x kali ia jatuh melintasi garis (x > 0), maka Aproksimasi π dapat ditentukan berdasarkan perhitungan :
Metode Monte Carlo lainnya untuk menghitung π adalah dengan menggambar sebuah lingkaran dalam sebuah persegi, dan meletakkan noktah-noktah secara acak di dalam perseegi. Perbandingan noktah di dalam lingkaran terhadap jumlah noktah total akan kira-kira sama dengan π/4.
Metode Monte Carlo untuk memperkirakan π sangat lambat dibandingkan metode lainnya, dan tidak pernah digunakan untuk memperkirakan π ketika diperlukan kecepatan atau akurasi.
MENCARI DIGIT PI (π) YANG AKURAT
Ada beberapa cara untuk mencari nilai Pi (π) yang akurat sesuai perkembangan zaman bersejarah, yaitu :
1. Menghitung Nilai Pi (π)
Piramida Giza Mesir yang dibangun pada tahun 2589–2566 SM, dibangun dengan kelilingnya sekitar 1760 Kubit dan tinggi sekitar 280 Kubit. Perbandingan antara keliling dengan tinggi piramida ini adalah 1760⁄280 ≈ 6,2857. Nilai ini mendekati 2π ≈ 6,2832. Berdasarkan rasio ini, beberapa ahli Mesir kuno menyimpulkan bahwa pendiri bangunan piramida ini memiliki pengetahuan akan π dan dengan sengaja mendesain piramida dengan rasio seperti ini. Beberapa ahli menyanggah hal tersebut dan menyimpulkan hal ini hanyalah kebetulan belaka karena tiada bukti lain apapun yang mendukungnya.
Pendekatan tertulis terhadap nilai π paling awal ditemukan di Mesir dan Babilonia, dengan nilai pendekatan berselisih lebih kurang 1 persen dari nilai sebenarnya. Sebuah lempeng liat dari Babilonia tahun 1900-1600 SM memuat penyataan mengenai geometri yang mengasumsikan π sebagai 25/8 = 3,1250. Di Mesir, Papirus Rhind yang berasal dari tahun 1650 SM (papirus ini sendiri merupakan salinan dari dokumen tahun 1850 SM) memiliki rumus luas lingkaran yang mengasumsikan nilai π sebagai (16⁄9)2 ≈ 3,1605.
Di India sekitar tahun 600 SM, catatan Sutra Shulba dalam Bahasa Sanskerta memuat nilai π sebesar (9785⁄5568)2 ≈ 3,088. Pada tahun 150 SM, sumber-sumber catatan dari India memperlakukan π sama dengan ≈ 3,1622.
2. Pendekatan / Estimasi Poligon
2. Pendekatan / Estimasi Poligon
Algoritma paling awal yang tercatat secara cermat menghitung nilai π adalah pendekatan geometri menggunakan Poligon. Algoritma ini ditemukan sekitar 250 SM oleh matematikawan Yunani Archimedes. Algoritma poligon ini mendominasi selama 1.000 Tahun, dan karenanya π kadang-kadang dirujuk juga sebagai "Konstanta Archimedes". Archimedes menghitung batas atas dan bawah π dengan menggambar poligon di luar dan di dalam sebuah lingkaran, dan secara perlahan melipatgandakan sisi-sisi poligon tersebut hingga mencapai 96-gon. Dengan menghitung keliling poligon-poligon tersebut, Archimedes membuktikan bahwa 223⁄71 < π < 22⁄7 (3,1408 < π < 3,1429). Batas atas Archimedes sekitar 22⁄7 membuat banyak orang percaya bahwa π sama dengan 22⁄7. Sekitar tahun 150, Ptolemaeus dalam Almagest-nya, memberikan nilai π sebesar 3,1416. Hasil ini kemungkinan dia dapatkan dari Archimedes ataupun dari Apollonius dari Perga. Para matematikawan kemudian menggunakan algoritme ini dan mencapai rekor 39 digit π pada tahun 1630 sebelum dipecahkan pada tahun 1699 menggunakan Deret tak Terhingga.
Pada zaman China kuno, nilai π adalah 3,1547 (sekitar Tahun 1 Masehi), (Tahun 100 M, sekitar 3,1623), dan 142/45 (Abad ke-3, sekitar 3,1556). Sekitar tahun 265, matematikawan dari Kerajaan : Wei, dan Liu Hui, menemukan Algoritma Iteratif Berbasis Poligon yang digunakan dengan 3072-gon untuk menghasilkan nilai π sebesar 3,1416. Liu kemudian menciptakan metode yang lebih cepat dan mendapatkan nilai 3,14 dengan menggunakan 96-gon. Matematikawan China Zu Chongzhi sekitar tahun 480 menghitung bahwa π ≈ 355⁄113 (Pecahan ini dinamakan pecahan Milü dalam Bahasa Tionghoa) dengan menggunakan algoritma Liu Hui dan menerapkannya menggunakan 12.288-gon. Nilai yang didapatkannya adalah 3,141592920... dan akurat sebanyak tujuh digit. Nilai pendekatan ini merupakan nilai yang paling akurat selama 800 tahun ke depan.
Astronom India Aryabhata menggunakan nilai 3,1416 dalam Āryabhaṭīya (tahun 499). Fibonacci pada tahun 1220 menghitung nilai π dan mendapatkan hasil 3,1418 menggunakan metode poligon.
Astronom Persia Jamshīd al-Kāshī menghasilkan 16 digit nilai π pada tahun 1424 menggunakan poligon bersisi 3×228,. Ini kemudian menciptakan rekor untuk 180 tahun. Matematikawan Prancis François Viète pada tahun 1579 mencapai 9 digit menggunakan poligon bersisi 3×217. Matematikawan Flandria mencapai 15 digit desimal pada tahun 1593. Pada tahun 1596, matematikawan Belanda Ludolph van Ceulenmencapai 20 digit, dan rekor ini dipecahkan oleh dirinya sendiri mencapai 35 digit. Ilmuwan Belanda Willebrord Snellius mencapai 34 digit pada tahun 1621, dan astronom Austria Christoph Grienberger mencapai 38 digit pada tahun 1630, adalah nilai terakurat yang didapatkan secara perhitungan manual menggunakan Pendekatan Poligon.
3. Deret tak Hingga
Deret tak hingga yang ditemukan di Eropa pertama kali adalah Perkalian tak Hingga (daripada Penjumlahan tak Hingga), yang ditemukan oleh matematikawan Prancis François Viète pada tahun 1593 :
Deret tak hingga kedua yang ditemukan di Eropa oleh John Wallis pada tahun 1655 juga merupakan perkalian tak hingga. Penemuan Kalkulus oleh Isaac Newton dan Gottfried Wilhelm Leibniz pada tahun 1660-an mendorong perkembangan banyak deret tak hingga untuk menghitung nilai π. Newton sendiri menggunakan deret arka sinus untuk menghitung π sampai dengan 15 digit pada tahun 1665 atau 1666.
Di Eropa, rumus Madhava ditemukan ulang oleh matematikawan Skotlandia James Gregory pada tahun 1671, dan oleh Leibniz pada tahun 1674 :
Rumus ini, yang disebut deret Gregory-Leibniz, sama dengan ketika dievaluasi bersama dengan z = 1. Pada tahun 1699, matematikawan Inggris Abraham Sharp menggunakan deret ini untuk menghitung π sampai dengan 71 digit, dan memecahkan rekor 39 digit sebelumnya. Deret Gregory-Leibniz cukup sederhana, namun berkonvergen sangat lambat, sehingga ia tidak digunakan pada zaman modern untuk menghitung π.
Pada tahun 1706, John Machin menggunakan deret Gregory-Leibniz untuk menghasilkan algoritme yang berkonvergen lebih cepat :
Machin mencapai 100 digit π dengan rumus ini. Beberapa matematikawan kemudian menciptakan beberapa varian yang digunakan untuk memecahkan rekor digit π secara suksesif. Rumus bak-Machin ini merupakan metode perhitungan digit π yang terbaik sebelum ditemukannya komputer. Rekor penemuan digit π terus dipecahkan menggunakan rumus ini selama 250, sampai dengan 620 digit oleh Daniel Ferguson pada tahun 1946. Nilai pendekatan ini dihasilkan tanpa menggunakan alat hitung apapun.
Matematikawan Britania William Shanks terkenal akan usahanya selama 15 tahun untuk menghitung nilai π sampai dengan 707 digit. Namun ia membuat kesalahan pada digit ke-528, membuat digit-digit selanjutnya salah.
4. Pecahan Kontinu (Continued Fraction)
Sama seperti semua bilangan irasional lainnya, π tidak dapat diwakilkan sebagai pecahan sederhana. Namun setiap bilangan irasional, termasuk π dapat diwakilkan menggunakan deret pecahan bersarang tak terhingga yang disebut sebagai Pecahan Kontinu :
Penghentian pecahan kontinu pada titik pembagian manapun akan memberikan nilai pendekatan π; dua pecahan 22/7 dan 355/113 secara historis digunakan sebagai pendekatan terhadap π. Walauapun pecahan kontinu yang sederhana (seperti pada contoh di atas) untuk π tidak memiliki pola-pola tertentu, matematikawan telah menemukan beberapa pecahan kontinu generalisasi yang memiliki pola tertentu, misalnya :
5. Dengan menggunakan Algoritma Iteratif
6. Dengan menggunakan Rumus Trigonometri
Perkembangan komputer yang pesat pada pertengahan abad ke-20 merevolusi perhitungan digit desimal π. Matematikawan Amerika John Wrench dan Levi Smith berhasil menghitung nilai pi sampai dengan 1.120 digit menggunakan kalkulator meja. Dengan menggunakan Deret Tak Terhingga Invers Tangen (arctan), sekelompok tim yang dipimpin oleh George Reitwiesner dan John von Neumann pada tahun yang sama berhasil mencapai 2.037 digit menggunakan komputer ENIAC dengan lama perhitungan selama 70 Jam. Rekor ini terus dipecahkan menggunakan deret arctan (7.480 digit pada tahun 1957; 10.000 digit pada tahun 1958; 100.000 digit pada tahun 1961), sampai dengan 1 juta digit pada tahun 1973.
Perkembangan lebih jauh sekitar tahun 1980 kemudian mempercepat kemampuan komputasi π. Pertama, penemuan Algoritma Iteratif baru yang lebih cepat daripada deret tak terhingga; dan kedua, penemuan Algoritme Perkalian Cepat yang mampu mengalikan bilangan besar dengan sangat cepat. Algoritme ini sangat penting karena waktu yang dihabiskan oleh komputasi komputer kebanyakan berkutat pada perkalian. Algoritme seperti ini contohnya Algoritme Karatsuba, Perkalian Toom-Cook, dan Metode berbasis Transformasi Fourier.
Algoritme Iteratif secara independen dipublikasikan pada tahun 1975-1976 oleh fisikawan Amerika Eugene Salamin dan ilmuwan Australia Richard Brent. Algoritme ini membuat komputasi digit pi bebas dari deret tak terhingga. Algoritme iteratif mengulangi perhitungan tertentu dengan tiap iterasi menggunakan hasil iterasi sebelumnya sebagai input dan setahap demi setahap menghasilkan nilai perhitungan yang berkonvergen ke nilai yang kita inginkan.
Algoritme iteratif digunakan secara meluas setelah tahun 1980 karena algoritme ini lebih cepat daripada algoritme deret tak terhingga. Manakala algoritme deret tak terhingga meningkatkan jumlah digit yang benar setiap suku, algoritme iteratif pada umumnya melipatgandakan jumlah digit yang benar pada setiap iterasi. Sebagai contohnya, algoritme Brent-Salamin menggandakan jumlah digit yang benar pada tiap iterasi. Pada tahun 1984, John dan Peter Borwein berhasil menemukan algoritme iteratif yang menggandaempatkan jumlah digit pada tiap iterasi; dan pada tahun 1987 berhasil menggandalimakan jumlah digit pada tiap iterasi. Metode iteratif digunakan oleh matematikawan Yasumasa Kanada untuk memecahkan beberapa rekor komputasi π antara tahun 1995 sampai dengan tahun 2002. Konvergensi yang sangat cepat ini memiliki kelemahannya sendiri, yakni memerlukan memori komputer yang jauh lebih besar daripada yang diperlukan oleh deret tak terhingga.
Dikutip dari Artikel : Majalah1000Guru.net
Caranya sebenarnya cukup mudah. Ada rumus cepat untuk menentukan pendekatan bilangan π ini sampai berapapun desimalnya! Yuk, kita lihat salah satu contohnya. Kita akan coba untuk menulis desimalnya sampai 3 kali lipat. Jika kita punya bilangan π yakni 3,14 (hanya dua desimal) dan kita ingin punya 6 desimal, kita bisa gunakan rumus mudah berikut :
Pada rumus di atas, p adalah nilai pendekatan π yang sudah kita punya (yakni 3,14). Dari mana asalnya rumus ini? Bukti logisnya seperti ini : Kita bisa ingat kembali bahwa sin(π) = 0. Jika nilai π yang kita masukkan hanya nilai pendekatannya saja, nilai sin p tidak akan bernilai nol sehingga p + sin(p) akan menghasilkan nilai π yang lebih presisi ! Jadi, jika p = 3,14, menggunakan kalkulator kita ambil 6 desimal dari p + sin(p) yakni 3,141592. Kita bisa ulang proses ini dengan p = 3.141592 untuk mendapatkan 3 kali lebih banyak desimal. Menarik, bukan?
Lebih jauh lagi, rumus untuk menghitung desimal bilangan π ternyata bukan hanya satu macam. Jika kita ingin mengetahui banyak digit desimalnya sampai 5 kali lipat kita bisa gunakan rumus berikut :
Untuk buktinya sendiri tidak semudah p+sin(p), tapi ide di balik pembuktiannya kurang lebih serupa. Jadi, jika ada pelajaran matematika berikutnya, kamu bisa unjuk kebolehan dengan menunjukkan nilai π dengan pendekatan lebih baik dari kalkulator biasamu !
[BONUS] Tetapi juga bisa mencari nilai pendekatan Pi (π) dengan menggunakan Hypeoperation Notation (Notasi Hiperoperasi)
Untuk lebih jelasnya :
a[1]b = a+b = a+1+1+...+1, dengan 1-nya diulang sebanyak "b" kali (Penjumlahan / Adition)
a[2]b = a*b = a+a+a+...+a, dengan a-nya diulang sebanyak "b" kali (Perkalian / Multiplication)
a[3]b = a^b = a*a*a*...*a, dengan a-nya diulang sebanyak "b" kali (Eksponensial / Exponentation)
a[4]b = a^^b = a^a^a^...^a, dengan a-nya diulang sebanyak "b" kali (Tetrasial / Tetration)
a[5]b = a^^^b = a^^a^^a^^...^^a, dengan a-nya diulang sebanyak "b" kali (Pentasial / Pentation)
a[6]b = a^^^^b = a^^^a^^^a^^^...^^^a, dengan a-nya diulang sebanyak "b" kali (Heksasial / Hexation)
(dan seterusnya)
Ingat :
a^^^^b = a^^^b = a^^b = a^b, 0≤b≤1
a^^^^b = a^^^b = a^^b = a^b, 0≤b≤1
a^^b = a^a^(b-1), 1≤b≤2
π ≈ 3 ^^^^ 1,03 ≈ 3,14186084712444 (Heksasi / Heksasial / Hexation)
3 ^^^^ 1,03 = 3 ^^^ 3 ^^^ (1,03 - 1)
= 3 ^^^ 3 ^^^ 0,3
= 3 ^^^ (3 ^ 0,3)
≈ 3 ^^^ 1,03350751204309
= 3 ^^^ 3 ^^^ 0,3
= 3 ^^^ (3 ^ 0,3)
≈ 3 ^^^ 1,03350751204309
= 3 ^^ 3 ^^ (1,03350751204309 - 1)
= 3 ^^ 3 ^^ 0,03350751204309
= 3 ^^ (3 ^ 0,03350751204309)
≈ 3 ^^ 1,03749770854944
= 3 ^ 3 ^ (1,03749770854944 - 1)
= 3 ^ 3 ^ 0,03749770854944
3 ^^^^ 1,03 ≈ 3,14186084712444 [TERBUKTI]
Atau untuk melihat digit lengkapnya :
3 ^^^^ 1,03
≈ 3,1418608471244454328872640978742
≈ 3,1418608471244454328872640978742
Mendekati nilai Pi (π) kan ??
*Keterangan tambahan :
Untuk mengetahui Operasi Hitung di atas Perpangkatan / Eksponensial, silahkan lihat di sini.
Untuk melihat postingan lamanya, silahkan lihat di sini.
Sekian Artikel ini, Pastinya anda juga pernah memakai Konstanta ini kan ?? Baik dari Jenjang SD, SMP, maupun SMA / SMK tetap terpakai Rumus Pi (π). Terima kasih.
Wassalamual'aikum Wr. Wb.






![{\displaystyle \scriptstyle {\sqrt[{3}]{31}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cd59a4a8f498c58e6c90241ca42e657e3cbe870)
![{\displaystyle \scriptstyle {\sqrt[{2}]{10}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bbf57ab4a4bf9e3cec3236ad4718beae814bb92)


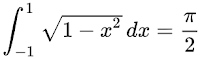



























Post a Comment