Assalammu‘alaikum wr. wb.
Hello gaes! Apakah kalian sudah mempersiapkan diri untuk menghadapi Ujian Sekolah (US)? Sebenarnya Ujian ini sebagai pengganti Ujian Nasional (UN) yang telah ditiadakan oleh Pemerintah akibat dari Pandemi COVID-19. Dan kali ini saya akan membagikan Kisi-kisi Ujian Sekolah (US) untuk Pelajaran Matematika (Wajib/Umum).
Berikut, inilah Materi Kisi-kisi US SMA untuk Pelajaran Matematika yang saya ambil dari beberapa Sumber di Internet. Dan juga Materi ini diambil dari Pelajaran Kelas 10, 11, dan sampai dengan Kelas 12.
1. Sifat-sifat Perpangkatan (Eksponensial)
Eksponen/Pangkat adalah suatu bentuk Perkalian dengan bilangan yang sama kemudian di ulang-ulang, yaitu Perkalian yang berulang-ulang.
2. Persamaan Kuadrat
Persamaan Kuadrat disini ada 2 Subtopik yaitu Fungsi Kuadrat (Titik Puncak) dan Persamaan Kuadrat.
Jika Titik Puncak-nya adalah  , maka Rumus Fungsi Kuadrat-nya adalah :
, maka Rumus Fungsi Kuadrat-nya adalah :
Jika Titik Potong sumbu x adalah  dan
dan  , maka Rumus Fungsi Kuadrat nya adalah :
, maka Rumus Fungsi Kuadrat nya adalah :
3. Subtitusi dan Eliminasi 2 Variabel / Sistem Persamaan Linear Dua Variabel (SPLDV)
Apabila kita mempunyai Sistem Persamaan linear dua variabel ke dalam variabel x dan y. langkah-langkah untuk menyelesaikan SPLDV ini adalah sebagai berikut :
Langkah 1 : Tentukan nilai x atau y menggunakan metode eliminasi dengan menjumlahkan atau mengurangkan.
Langkah 2 : Substitusikan nilai x atau y yang diperoleh pada langkah 1 ke salah satu persamaan yang diperoleh dan selesaikanlah persamaan itu.
Langkah 3 : Tulislah himpunan penyelesaiannya.
[Untuk selengkapnya, silahkan lihat di sini (Quipper Blog).]
4. Pertidaksamaan Eksponensial
Hal yang membedakan bentuk persamaan dengan bentuk Pertidaksamaan adalah Tanda Penghubung-nya saja. Jadi sebenarnya, bentuk-bentuk persamaan eksponen yang sudah dijabarkan di atas tadi juga merupakan bentuk Pertidaksamaan Eksponen. Tapi, tanda Penghubungnya berubah menjadi “<, >, ≤, ≥, atau ≠”.
 |
| Sumber : Blog Ruangguru |
5. Fungsi Komposisi dan Invers
Fungsi Komposisi adalah gabungan dari beberapa fungsi yang ada. Fungsi Komposisi disimbolkan dengan “ o “ (Bundaran). Contoh gabungan dari dua Fungsi yaitu f o g (x) = f((g(x)) dan g o f(x) = g(f(x)). Artinya ada dua gabungan yaitu fungsi f(x) dengan fungsi g(x).
Suatu Fungsi memiliki suatu Invers. Invers adalah suatu proses pembalikan suatu Fungsi asalnya. Fungsi Invers dan disimbolkan dengan pangkat tanda -1 contoh : f-1(x) dibaca: Invers dari fungsi f(x). Sebagai contoh Himpunan a terdiri 3 Elemen yaitu {a,b,c} dan Himpunan B terdiri dari 3 Elemen yaitu {1,2,3}.
Misalnya Fungsi (x) adalah terdiri dari 5 pria berkulit hitam dan 1 wanita berkulit putih maka fungsi inversnya adalah 5 wanita berkulit hitam di belakang dan 1 pria berkulit hitam di posisi depan. Strategi penentuan fungsi invers dari fungsi y = f(x) dapat ditembuh dengan langkah-langkah berikut ini :
Nyatakan x sebagai fungsi y, yaitu x = f-1(x)
Ganti y dengan x dan x dengan y, sehingga y = f-1(x) merupakan invers fungsi dari y = f(x)
[Untuk selengkapnya, silahkan lihat di sini (Quipper Blog) atau di sini (Studiobelajar.com).]
6. Linear Programing (Model Matematika)
Program Linear atau Linear Programing adalah suatu metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimal atau minimum) diperoleh dari nilai dalam suatu himpunan penyelesaiaan persoalan linear. Di dalam persoalan linear terdapat fungsi linear yang bisa disebut sebagai Fungsi Objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan Sistem Pertidaksamaan Linear.

7. Matriks/Matrix
Matriks adalah susunan kumpulan bilangan yang di atur dalam baris dan kolom berbentuk persegi panjang. Matriks di cirikan dengan elemen-elemen penyusun yang diapit oleh tanda kurung siku [ ] atau tanda kurung biasa ( ).
Ukuran sebuah matrik dinyatakan dalam satuan ordo, yaitu banyaknya baris dan kolom dalam matriks tersebut. Ordo merupakan karakteristik suatu matriks yang menjadi patokan dalam Oprasi-oprasi antar matriks. Matriks pada umumnya di simbolkan seperti berikut ini :
Keterangan :
A = Nama Matriks
m = Banyak Baris
n = Banyak Kolom
m x n = Ordo Matriks
Am x n = Elemen Matriks Baris ke-m Kolom ke-n.
8. Deret Aritmatika & Geometri
Sebenarnya di bagian ini terdapat 2 Subbab yaitu Deret Aritmatika & Geometri. Barisan Aritmetika merupakan barisan bilangan dengan pola yang tetap berdasarkan operasi penjumlahan dan pengurangan. Selisih antara dua suku berurutan pada barisan aritmetika disebut beda yang dilambangkan dengan b. Rumus untuk menentukan beda pada barisan aritmetika adalah sebagai berikut.
Keterangan :
b = Beda;
Un = Suku ke-n;
Un+1 = Suku sebelum Suku ke-n; dan
n = Banyaknya Suku.
Sedangkan Barisan Geometri merupakan barisan bilangan yang hasil bagi antara dua suku berurutannya selalu sama atau tetap. Perbandingan (hasil bagi) antara dua suku berurutan pada barisan geometri disebut dengan rasio yang dilambangkan dengan r.
Keterangan :
r = Rasio;
Un = Suku ke-n;
Un-1= Suku sebelum suku ke-n; dan
n = Banyaknya suku.
9. Bangun Ruang pada Kubus
Materi Dimensi Tiga mencakup tentang Jarak, Sudut pada Bangun Ruang. Untuk selengkapnya, bisa membacanya di sini. Atau kalian bisa membacanya di Blog ini tentang Bangun Ruang Kubus.
10. Diagonal Bangun Ruang Balok
Diagonal Bidang suatu Balok adalah Ruas Garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang atau sisi balok. Untuk memahami definisi tersebut coba perhatikan bidang TUVW pada gambar di bawah ini.
Atau kalian bisa membacanya di Blog ini tentang Diagonal Bangun Ruang Balok.
11. Aturan Sinus dan Cosinus
Anda pasti sudah tidak asing lagi dengan kata Sinus (sin) dan Cosinus (cos), bukan? Dalam trigonometri, ternyata Sinus dan Cosinus mempunyai aturan tersendiri, khususnya pada segitiga. Apa itu aturannya? Perbandingan panjang sisi dengan sudut pada segitiga serta menghitung luas segitiga dilakukan dengan menggunakan Prinsip Trigonometri.
12. Trigonometri
Trigonometri (dari Bahasa Yunani trigonon (τρίγωνον) = tiga sudut dan metron (μέτρον) = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segitiga dan Fungsi Trigonometrik seperti Sinus (sin), Cosinus (cos), Tangen (tan), Cotangen (cot), Sekan (sec), dan Cosecan (csc). Di Inzaghi's Blog juga ada Artikel yang membahas tentang Rumus Trigonometri.
13. Nilai pada Limit (Aljabar)
Limit merupakan sebuah konsep matematika dimana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu.
Dalam pengoperasian Limit Fungsi Aljabar, terdapat beberapa hukum atau teorema limit yang perlu diperhatikan. Jika k konstanta, fungsi f dan fungsi g adalah fungsi-fungsi memiliki nilai limit yang mendekati bilangan c, maka :
Ada 3 (Tiga) Metode dalam mengerjakan Limit Fungsi Aljabar, yaitu Metode Subtitusi, Metode Pemfaktoran, dan Metode Perkalian dengan Akar Sekawan.
14. Integral
Sebelumnya Inzaghi's Blog juga pernah membahas Artikel tentang Integral. Ada Integeral Tentu (Definite Integral) dan juga Integral Tak Tentu (Indefinite Integral). Oleh karena itu, Rumus umum Integral dinyatakan sebagai berikut.

15. Turunan
Sebelumnya Inzaghi's Blog juga pernah membahas Artikel tentang Turunan. Turunan atau Diferensial merupakan kebalikannya dari Integral. Misalkan y adalah Fungsi dari x atau ) . Turunan (Diferensial) dari y terhadap x. Dinotasikan dengan :
. Turunan (Diferensial) dari y terhadap x. Dinotasikan dengan :
16. Persamaan Garis Singgung
Di Blog ini juga pernah membahas tentang Persamaan Garis Singgung. Untuk melihatnya, bisa lihat di sini. Jika terdapat Kurva ) disinggung oleh sebuah garis di titik
disinggung oleh sebuah garis di titik ) maka gradien garis singgung tersebut bisa dinyatakan dengan
maka gradien garis singgung tersebut bisa dinyatakan dengan ) . Sementara itu
. Sementara itu 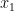 dan
dan 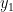 memiliki hubungan
memiliki hubungan ) . Sehingga Persamaan Garis Singgung-nya bisa dinyatakan dengan
. Sehingga Persamaan Garis Singgung-nya bisa dinyatakan dengan ) .
.
Jadi intinya jika kita akan mencari Persamaan Garis Singgung suatu Kurva jika diketahui Gradien-nya m dan menyinggung di Titik ) maka kita gunakan Persamaan
maka kita gunakan Persamaan ) .
.
17. Statistika (Kuartil, Modus, Simpangan Rata-rata, Simpangan Baku, dan Ragam Variasi)
Beberapa Bulan yang lalu, Inzaghi's Blog juga pernah membahas tentang Rumus-rumus dari Statistika. Memang di materi ini ada beberapa Subbab seperti Kuartil, Modus, Simpangan Rata-rata, Simpangan Baku, dan Ragam Variasi. Silahkan lihat dan dibaca kembali tentang Topik ini.
18. Menggambar Diagram Lingkaran
Diagram Lingkaran merupakan diagram yang menunjukkan data atau hasil angka-angka dalam bentuk lingkaran. Diagram memiliki tipe yang berbeda, misalnya, diagram batang, diagram garis, dan diagram lingkaran. Dan untuk Topik ini juga banyak sumbernya misalkan dari YouTube.
19. Permutasi dan Kombinasi
Dan Minggu kemarin, Inzaghi's Blog juga sempat mem-Posting Artikel tentang Permutasi dan Kombinasi. Silahkan lihat dan dibaca kembali tentang Topik ini.
Mohon maaf apabila ada sedikit Kesalahan dalam memberikan materi yang kurang jelas dan juga memberikan Link atau Dokumen yang terkait. Terima Kasih 😀👍 :)
Wassalammu‘alaikum wr. wb.






Post a Comment