[#BelajarDiRumah] Inilah Pengertian, Bentuk Umum, Materi, hingga Contoh Soal tentang Turunan (+ Video Pembelajaran)

May 31, 2020

Assalammu‘alaikum wr. wb.

Hello gaes! Apakah kalian juga termasuk Phobia Matematika? Kali ini jangan takut untuk berhitung. Di pembahasan kali ini saya akan menjelaskan tentang Rumus Turunan.

Rumus Turunan (Diferensial)

Sumber Materi : Tomyherawansman48jkt.blogspot.com dan juga dari sumber yang lain

Turunan (Diferensial) adalah Pengukuran terhadap bagaimana Fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan Turunan disebut Diferensiasi.

Misalkan y adalah Fungsi dari x atau $y = f(x)$ . Turunan (Diferensial) dari y terhadap x. Dinotasikan dengan :

$\frac{dy}{dx} = \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{f(x + \Delta x) - f(x))}{\Delta x}$

RUMUS DAN PEMBAHASAN MATERI TURUNAN (BESERTA CONTOH SOAL)

1. Rumus Dasar

Sebelum melanjutkan untuk membaca, saksikan terlebih dahulu secara saksama Video dari Youtube yang ada di bawah ini :

a.) Turunan Pertama

Inilah Rumus Turunan berserta Contohnya.

Jika $y = C \cdot x^{n}$ dengan C dan n konstanta real, maka : $\frac{dy}{dx} = C n \cdot x^{n-1}$

Contoh :

1.) $y = 2x^{4}$ maka $\frac{dy}{dx} = 2 \cdot 4 x^{4-1} = 8x^{3}$

2.) $y = 2$ maka $\frac{dy}{dx} = 0$

3.) $f(x)+g(x)$ maka $\frac{dy}{dx} = f'(x)+g'(x)$

CONTOH SOAL :

• $f(x)= \frac{2}{3}x^{3}+2x^{2}+1$ , tentukan Turunan Pertama dari $f(x)$ atau $f'(x) = \cdots$

• $f(x)= \frac{3}{x^{3}}+2x$ , tentukan Turunan Pertama dari $f(x)$ atau $f'(x) = \cdots$

• $f(x)= 3\sqrt{x}+1$ , tentukan Turunan Pertama dari $f(x)$ atau $f'(x) = \cdots$

b.) Turunan Kedua

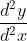Turunan kedua $y = f(x)$ terhadap x dinotasikan dengan $\frac{d^{2}y}{d^{2}x}$ atau y". Turunan kedua diperoleh dengan menurunkan turunan pertama.

Contoh :

CONTOH SOAL :

• Turunan Kedua dari fungsi $y=2x^{2}-3x+5$ adalah ....

2. Sifat-sifat Turunan

Ataupun juga bisa melihat dari Situs lain di sini untuk mengetahui dar Sifat Turunan.

Dalam mencari turunan, seringkali kita menjumpai dua fungsi atau lebih yang dijumlahkan, dikurangkan, dikalikan dan dibagikan. Untuk memudahkan perhitungan ini, dibuatlah sifat-sifat turunan.

Jika u dan v adalah fungsi dalam x, dan c adalah Konstanta, maka berlaku :

1.) $f(x) = u + v$ maka $f'(x) = u' + v'$

2.) $f(x) = u - v$ maka $f'(x) = u' - v'$

3.) $f(x) = c \cdot u$ maka $f'(x) = c \cdot u'$

4.) $f(x) = u \cdot v$ maka $f'(x) = u'v + uv'$

5.) $f(x) = \frac{u}{v}$ maka $f'(x) = \frac{u'v - uv'}{v^{2}}$

Contoh :

• $f(x) = 2x^{2} - 3x + 4$

Pembahasan :

$f'(x) = (2x^{2})' - (3x)' + (4)'$

$= 2 \cdot 2x^{2-1} - 3$

$= 4x - 3$

• $f(x) = (x^{3}+5x^{2}-4x+2)(x^{2}-4x+7)$

Pembahasan : Misalkan saja $u(x) = x^{3}+5x^{2}-4x+2$ dan $v(x) = x^{2}-4x+7$ , maka :

$u'(x) = 3x^{2} + 10x - 4$ dan $v'(x) = 2x - 4$

$f'(x) = u'v + uv'$

$= (3x^{2}+10x-4)(x^{2}-4x+7)+(3x^{3}+5x^{2}-4x+2)(2x-4)$

$= (3x^{4}-2x^{3}-23x^{2}+86x-28) + (6x^{4}-2x^{3}-28x^{2}+20x-8)$

$= 3x^{4}+6x^{4}-2x^{3}-2x^{3}-23x^{2}-28x^{2}+86x+20x-28-8$

$= 9x^{4} - 4x^{3} - 51x^{2} + 106x - 36$

• $f(x) = \frac{4x^{2}+7}{3x-5}$

Pembahasan : Misalkan saja $u(x) = 4x^{2}+7$ dan $v(x) = 3x-5$ , maka :

$u'(x) = 8x$ dan $v'(x) = 3$

$f'(x) = \frac{u'v - uv'}{v^{2}}$

$= \frac{8x(3x-5) - (4x^{2}+7) \cdot 3}{(3x-5)^{2}}$

$= \frac{(24x^{2}-40x) - (12x^{2}+21)}{(3x-5)^{2}}$

$= \frac{24x^{2}-40x - 12x^{2}+21}{9^{2}-30x+25}$

$= \frac{12x^{2}-40x-21}{9^{2}-30x+25}$

CONTOH SOAL LAINNYA :

• $f(x) = \frac{3x}{3-5x}$ , tentukan Turunan Pertama dari $f(x)$ atau $f'(x) = \cdots$

• $f(x) = (2x+2)(x^{2}+2x+1)$ , tentukan Turunan Pertama dari $f(x)$ atau $f'(x) = \cdots$

Berikut, saksikan secara saksama Video dari Youtube yang ada di bawah ini :

3. Rumus-rumus Dasar yang berhubungan dengan Turunan

a.) Turunan Fungsi Identitas

Contoh :

$f(x) = x$ maka $f'(x) = 1$

$f(x) = 2x$ maka $f'(x) = 2$

$f(x) = 3x$ maka $f'(x) = 3$

$f(x) = 4x$ maka $f'(x) = 4$

$f(x) = n \cdot x$ maka $f'(x) = n$

b.) Turunan Fungsi Eksponen

Contoh :

$f(x) = x^{n}$ maka $f'(x) = n \cdot x^{n-1}$

$f(x) = x^{2}$ maka $f'(x) = 2x^{2-1} = 2x$

$f(x) = x^{5}$ maka $f'(x) = 5x^{5-1} = 5x^{4}$

$f(x) = x^{10}$ maka $f'(x) = 10x^{10-1} = 10x^{9}$

$f(x) = x^{100}$ maka $f'(x) = 100x^{100-1} = 100x^{99}$

c.) Turunan Hasil Konstanta dari Fungsi

Contoh :

$f(x) = ax^{n}$ maka $f'(x) = n \cdot ax^{n-1}$

$f(x) = 3x^{2}$ maka $f'(x) = 2 \cdot 3x^{2-1} = 6x$

$f(x) = 40x^{5}$ maka $f'(x) = 5 \cdot 40x^{5-1} = 200x^{4}$

$f(x) = 25x^{12}$ maka $f'(x) = 12 \cdot 25x^{12-1} = 300x^{11}$

$f(x) = 6x^{20}$ maka $f'(x) = 20 \cdot 6x^{20-1} = 120x^{19}$

4. Aturan Rantai Turunan [BONUS]

Ataupun juga bisa melihat dari Situs lain di sini untuk mengetahui dar Aturan Rantai Turunan.

Aturan Rantai pada soal turunan sangatlah penting. Hal ini disebabkan hampir kebanyakan persamaan dalam penerapan Kalkulus (Pada Pelajaran Fisika), mengandung fungsi didalam fungsinya. Contoh fungsi dalam fungsi ini adalah. Misalkan kita memiliki fungsi $f(g(x))$ . Dalam fungsi f terkandung fungsi lain berbentuk $g(x)$ . Permasalahan yang kita hadapi sekarang adalah bagaimana bentuk turunan dari fungsi $f(g(x))$ ini. Nah dengan aturan rantai kita dapat mengerjakan permasalahan semacam ini. Adapun bentuk aturan rantai adalah sebagai berikut.

Aturan Rantai :

Jika f dan g merupakan fungsi yang dapat dideferensialkan (Turunkan). $F = f \circ g$ adalah fungsi dengan definisi $F(x) = f(g(x))$ . Maka F dapat dideferensialkan menjadi sebagai berikut.

Apabila digunakan notasi Leibniz, dengan y = f(u) dan u = g(x). Aturan rantai dapat ditlis ulang menjadi.

Nah sekarang bentuk aturan rantai ini akan kita gunakan untuk mengerjakan contoh-contoh soal berikut.

Kita memiliki sebuah fungsi F(x) = (x^3+4x)^7. Dalam fungsi pangkat terdapat fungsi dengan bentuk x^3+4x. Kita definisikan u = x^3+4x . Sehingga dengan menerapkan aturan rantai, maka dapat kita peroleh.

CONTOH SOAL LAINNYA :

RUMUS DAN PEMBAHASAN MATERI TENTANG FUNGSI NAIK TURUN (BESERTA CONTOH SOAL)

Ataupun juga bisa melihat dari Situs lain di sini untuk mengetahui dar Fungsi Naik Turun.

Sebelum melanjutkan untuk membaca, saksikan terlebih dahulu secara saksama Video dari Youtube yang ada di bawah ini :

Dari grafik diatas dapat dilihat bahwa fungsi $f(x)$ naik pada interval

x < a

atau

x > b

dan turun pada Interval. Selain dengan melihat secara Visual pada grafik,

Interval Naik atau turunnya suatu fungsi dapat ditentukan dari turunan pertama fungsi tersebut.

Jika $f'(x)>0$ untuk semua x yang berada pada Interval I, maka f naik pada I.
Jika f'(x) < 0 untuk semua x yang berada pada Interval I, maka f turun pada I.

Definisi 1 :

Jika diberikan fungsi f dengan daerah asal Df dan x = c merupakan anggota Df, maka berlaku hubungan sebagai berkut :

$f(c)$ adalah Nilai Maksimum fungsi f pada Df jika $f(c) \geq f(x)$ untuk semua x di Df.
$f(c)$ adalah Nilai Minimum fungsi f pada Df jika $f(c) \leq f(x)$ untuk semua x di Df.
$f(c)$ adalah Nilai Ekstrim fungsi f pada Df jika $f(c)$ adalah Nilai Maksimum atau Minimum fungsi f di Df.

Definisi 2 :

Jika diberikan fungsi f dengan daerah asal Df dan interval (a,b) merupakan himpunan bagian dari Df, maka berlaku hubungan sebagai berkut :

$f(c)$ adalah Nilai Maksimum Lokal fungsi f pada Interval (a,b) yang memuat c jika $f(c)$ adalah nilai maksimum fungsi f pada (a,b).
$f(c)$ adalah Nilai Minimum Lokal fungsi f pada Interval (a,b) yang memuat c jika $f(c)$ adalah nilai minimum fungsi f pada (a,b).
$f(c)$ adalah Nilai Ekstrim Lokal fungsi f jika $f(c)$ adalah Nilai Maksimum lokal atau nilai minimum lokal fungsi f.

Lalu, kapan terjadi Nilai Ekstrim Lokal?

Kalian dapat menggunakan uji turunan pertama untuk menentukan Nilai Ekstrim Lokal.

Jika Fungsi f Kontinu pada selang terbuka (a,b) yang memuat x = c, maka berlaku hubungan sebagai berikut :

Jika $f'(x)>0$ untuk semua nilai x dalam selang (a,c) dan f'(x) < 0 untuk semua nilai x dalam selang (c,b), maka $f(c)$ merupakan Nilai Maksimum lokal f.
Jika $f'(x)<0$ untuk semua nilai x dalam selang (a,c) dan $f'(x)>0$ untuk semua nilai x dalam selang (c,b), maka $f(c)$ merupakan Nilai Minimum lokal f.
Jika $f(c)$ pada selang (a,c) dan (c,b), maka $f(c)$ bukan merupakan Nilai Ekstrim Lokal f.

Agar lebih jelas, mari perhatikan gambar di bawah ini.

Contoh Soal (Sumber : Smatika.blogspot.com) :

1. Jika f(x) = x² − 6x + 8, tentukan Interval f(x) naik dan Interval f(x) turun!

Jawab :

   f '(x) = 2x − 6

   f(x) naik ⇒ f '(x) > 0
   ⇔ 2x − 6 > 0
   ⇔ 2x > 6
   ⇔ x > 3

   f(x) turun ⇒ f '(x) < 0
   ⇔ 2x − 6 < 0
   ⇔ 2x < 6
   ⇔ x < 3

Jadi f(x) naik pada interval x > 3 dan turun pada Interval x < 3.

2. Fungsi f(x) = 2x³ − 3x² − 36x naik pada Interval ...

Pembahasan :

   f '(x) = 6x² − 6x − 36

   f(x) naik ⇒ f '(x) > 0
   ⇔ 6x² − 6x − 36 > 0

   Pembuat nol :
   6x² − 6x − 36 = 0
   x² − x − 6 = 0
   (x + 2)(x − 3) = 0
   x = −2 atau x = 3

Jadi f(x) naik pada interval x < −2 atau x > 3

3. Fungsi f(x) = x⁴ − 8x³ + 16x² + 1 turun pada interval ...

Pembahasan :

   f '(x) = 4x³ − 24x² + 32x

   f(x) turun ⇒ f '(x) < 0
   ⇔ 4x³ − 24x² + 32x < 0

   Pembuat nol :
   ⇔ x³ − 6x² + 8x = 0
   ⇔ x (x² − 6x + 8) = 0
   ⇔ x (x − 2)(x − 4) = 0
   ⇔ x = 0 atau x = 2 atau x =4

Jadi f(x) turun pada Interval

x < 0

atau

2 < x < 4

CONTOH SOAL LAINNYA :

• $y = x^{3}+3x^{2}$ , Fungsi akan naik pada Interval….

• Grafik Fungsi $f(x) = x^{3}+x^{2}-5x+7$ akan naik pada Interval….

RUMUS DAN PEMBAHASAN MATERI TENTANG PERSAMAAN GARIS SINGGUNG KURVA (BESERTA CONTOH SOAL)

Sebelum melanjutkan untuk membaca, saksikan terlebih dahulu secara saksama Video dari Youtube yang ada di bawah ini :

Jika terdapat Kurva $y = f(x)$ disinggung oleh sebuah garis di titik $(x_{1}, y_{1})$ maka gradien garis singgung tersebut bisa dinyatakan dengan $m = f'(x_{1})$ . Sementara itu $x_{1}$ dan $y_{1}$ memiliki hubungan $y_{1} = f(x_{1})$ . Sehingga Persamaan Garis Singgung-nya bisa dinyatakan dengan $y-y_{1} = m(x-x_{1})$ .

Jadi intinya jika kita akan mencari Persamaan Garis Singgung suatu Kurva jika diketahui Gradien-nya m dan menyinggung di Titik $(x_{1}, y_{1})$ maka kita gunakan Persamaan $y-y_{1} = m(x-x_{1})$

Sedangkan jika diketahui 2 Titik, misalnya Sedangkan jika diketahui 2 titik, misalnya $(x_{1},y_{1})$ dan $(x_{2},y_{2})$ maka untuk mencari Persamaan Garis Singgung dari Dua Titik tersebut kita dapat gunakan Persamaan $(x_{1},y_{1})$ dan $(x_{2},y_{2})$ dan dapat kita gunakan Persamaan sebagai berikut :

$\frac{y-y_{1}}{y_{2}-y_{1}} = \frac{x-x_{1}}{x_{2}-x_{1}}$

CONTOH SOAL :

CONTOH SOAL TENTANG APLIKASI TURUNAN

Berikut, inilah Contoh Soal dari Aplkasi Turunan dalam Kehidupan sehari-hari.

Demikianlah semoga membantu khususnya untuk menyelesaikan soal Mata Pelajaran Matematika Wajib Kelas 11. Dan Nantikan pembahasan selanjutnya tentang Integral.

Mohon maaf apabila ada sedikit Kesalahan, baik itu Salah Kata, ataupun Salah menulis Rumus.Terima Kasih 😀👍 :)

Wassalammu‘alaikum wr. wb.

Inzaghi's Blog (Legacy)

[#BelajarDiRumah] Inilah Pengertian, Bentuk Umum, Materi, hingga Contoh Soal tentang Turunan (+ Video Pembelajaran)

Ads